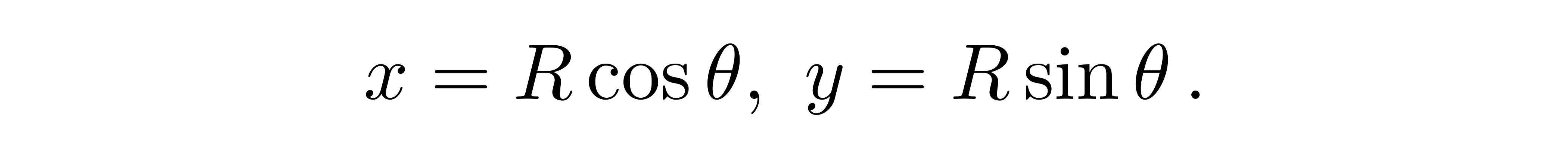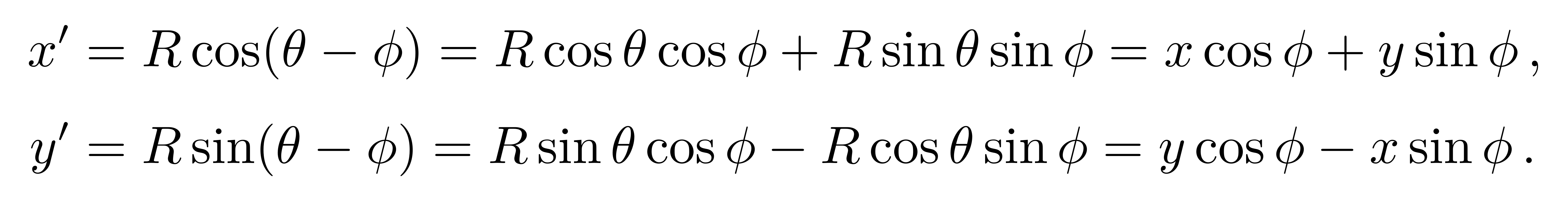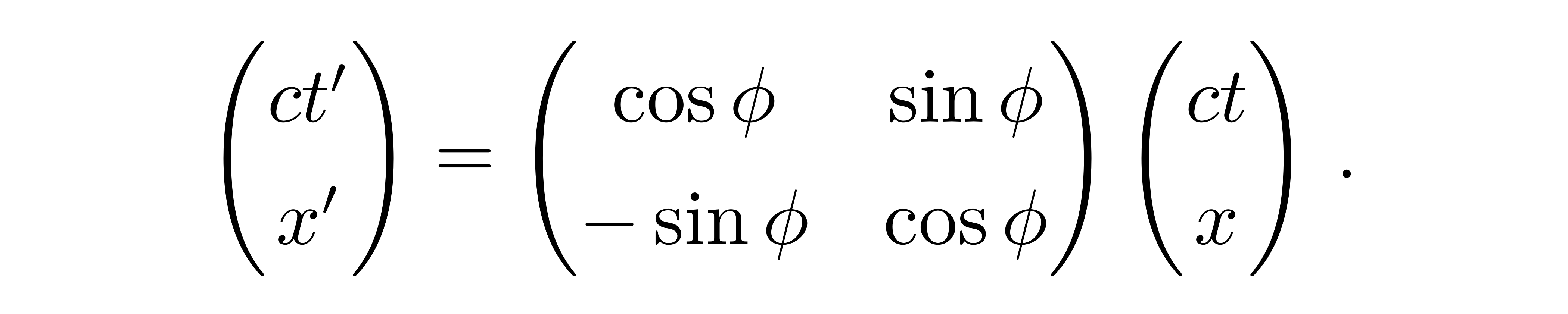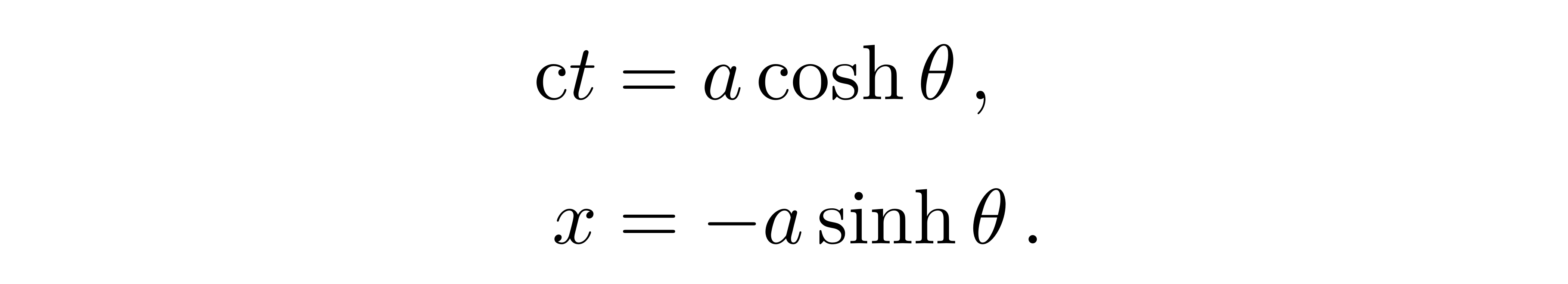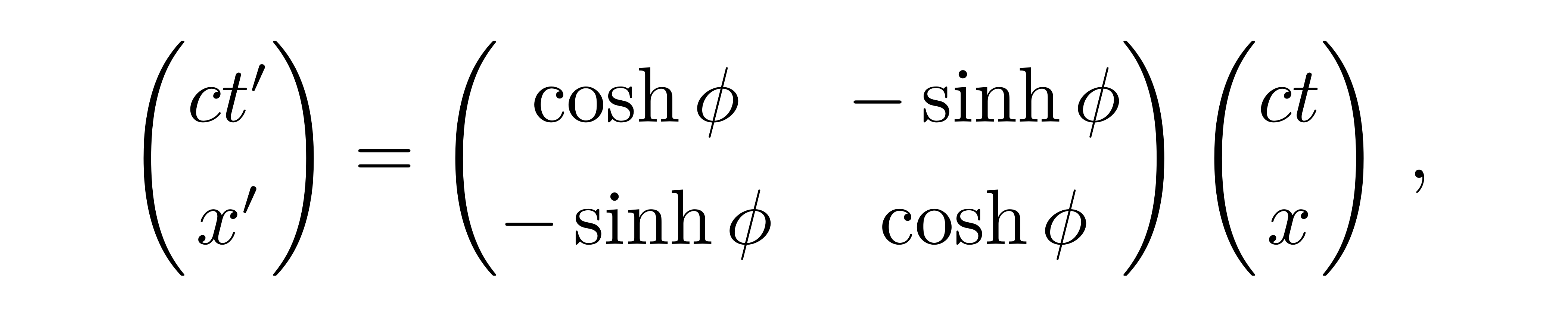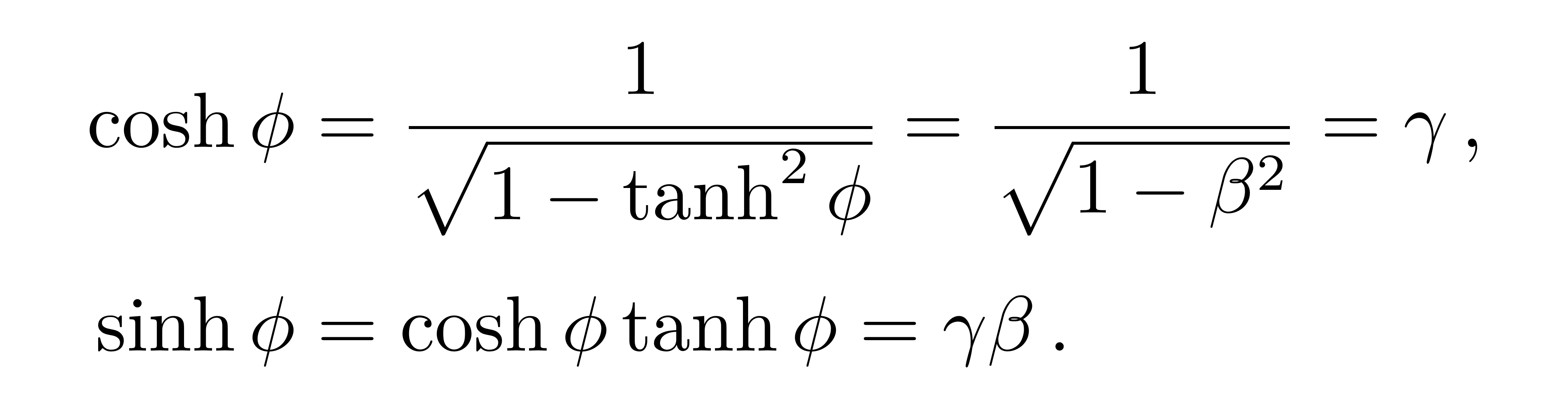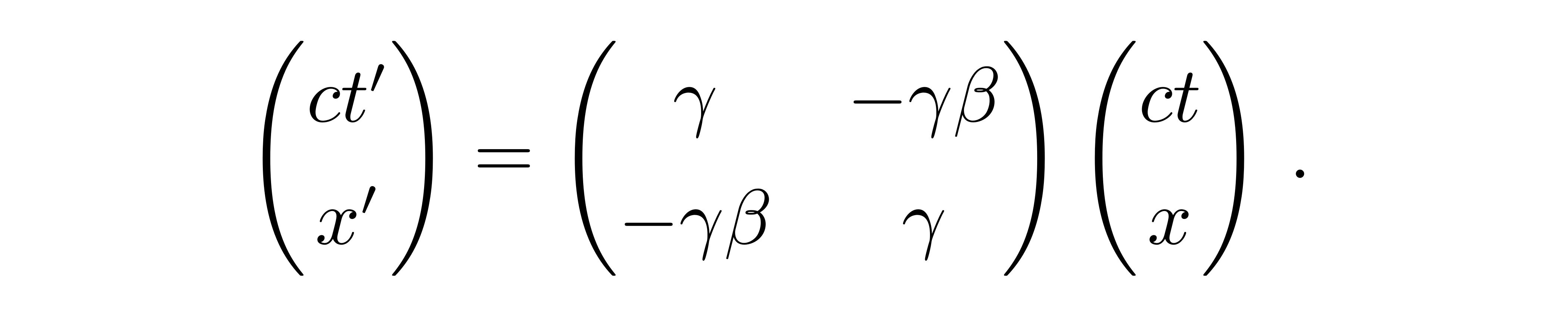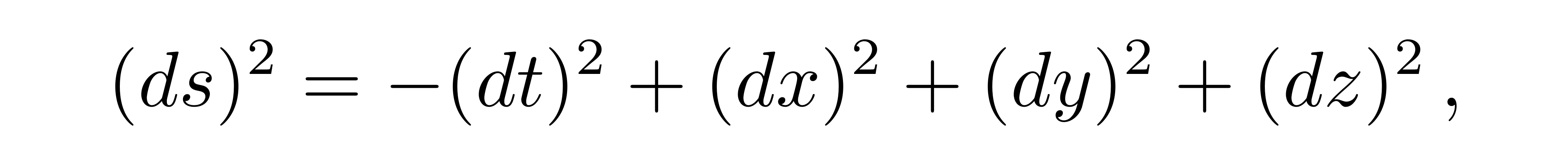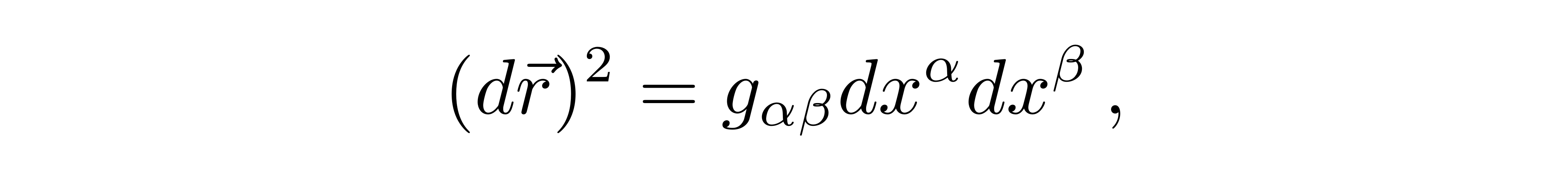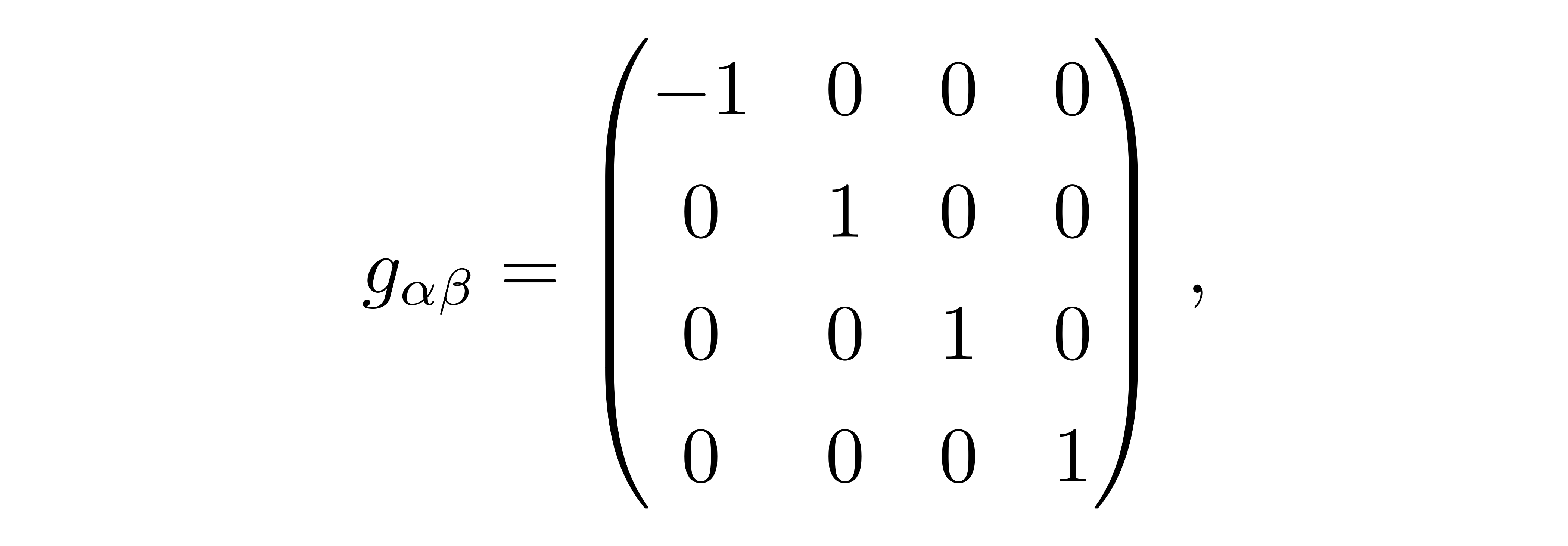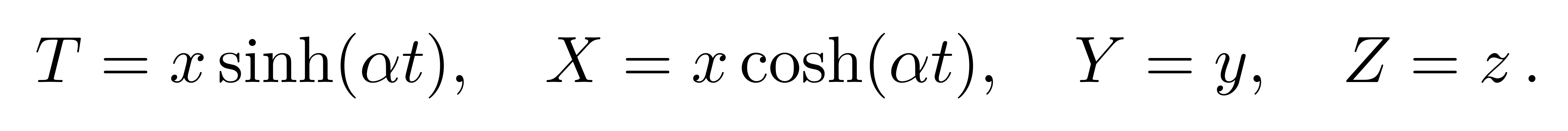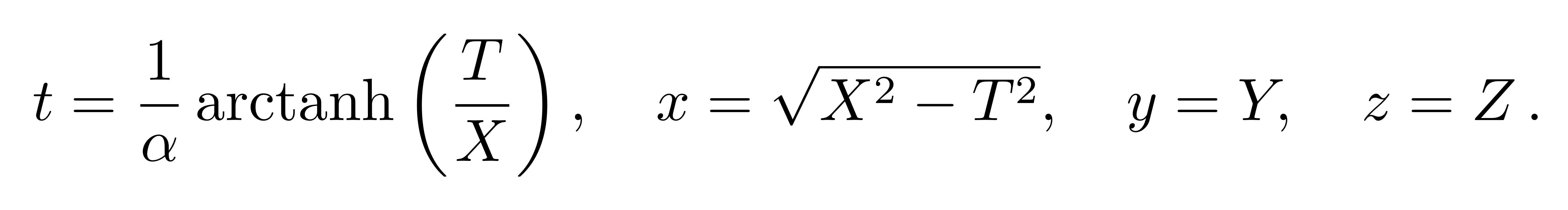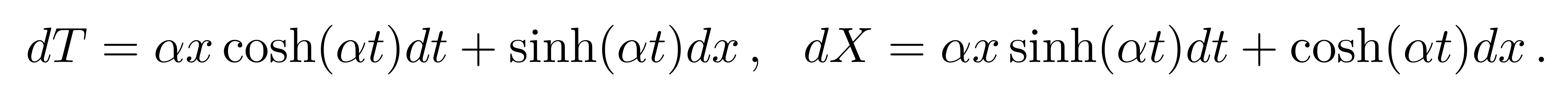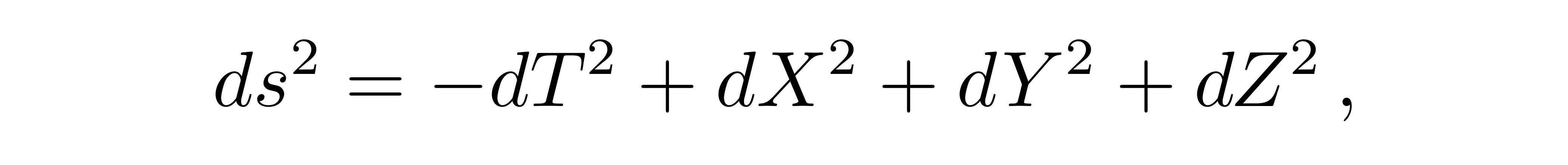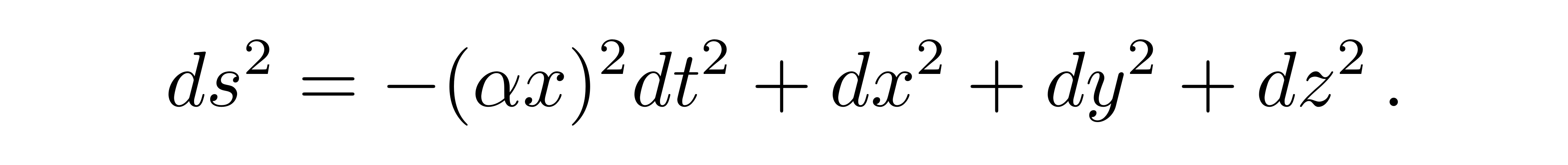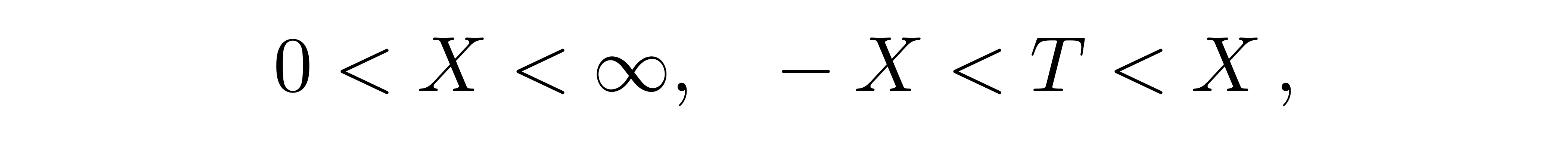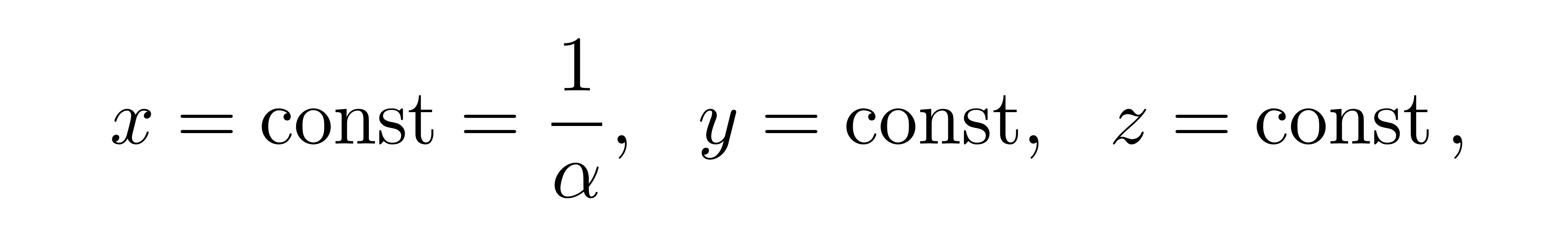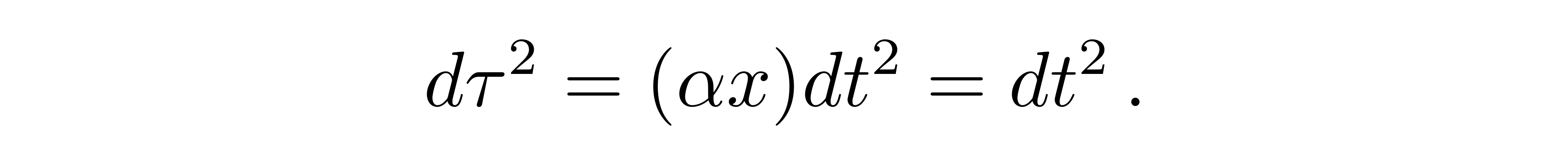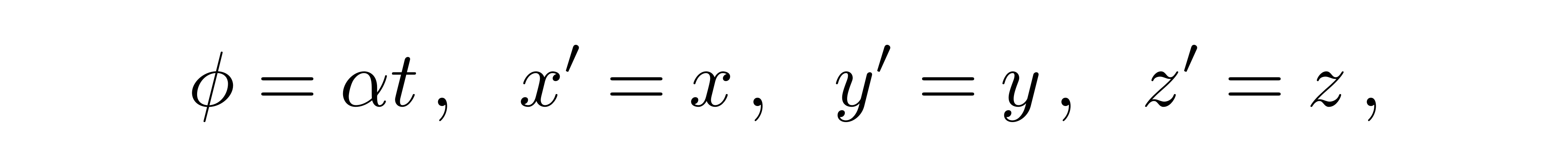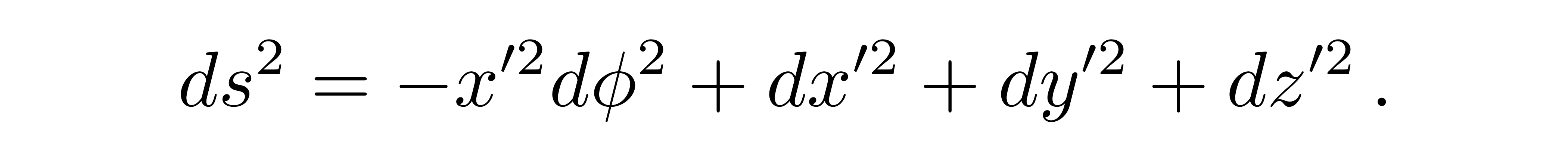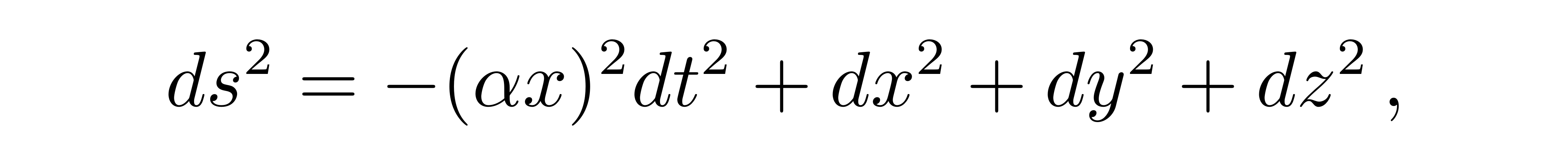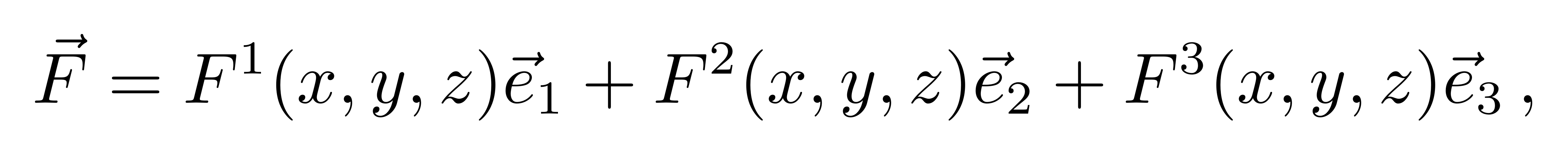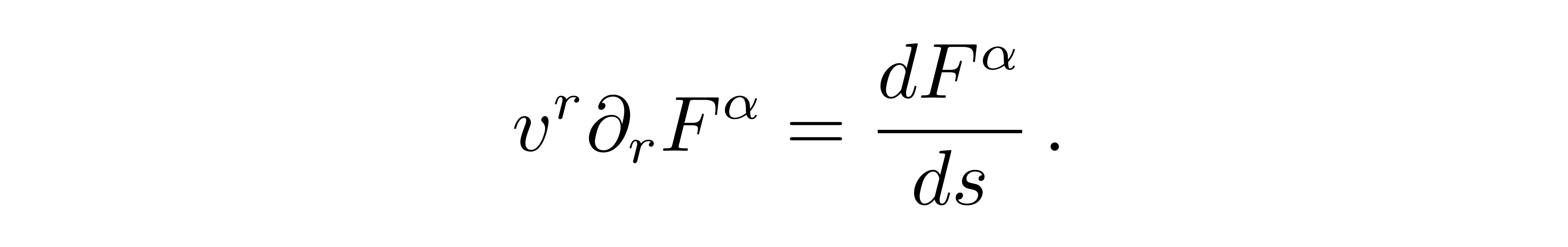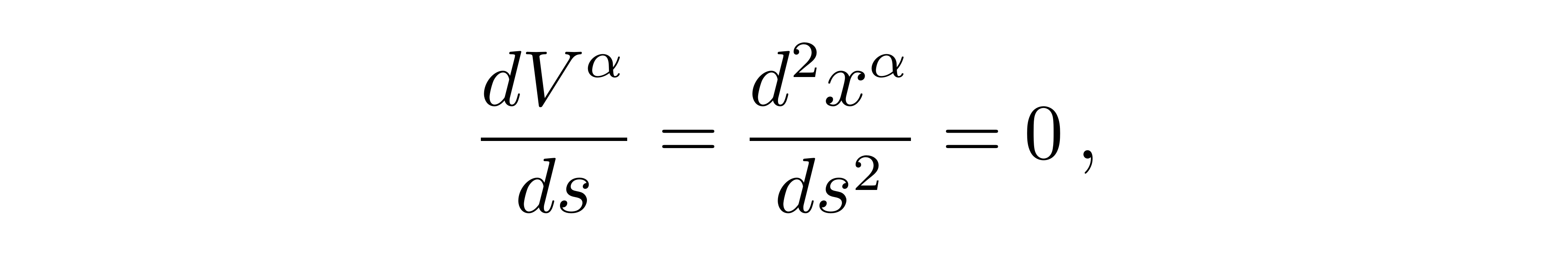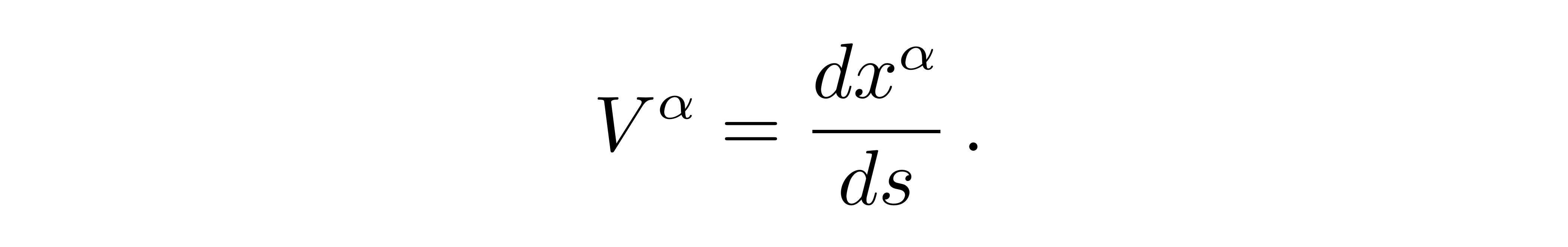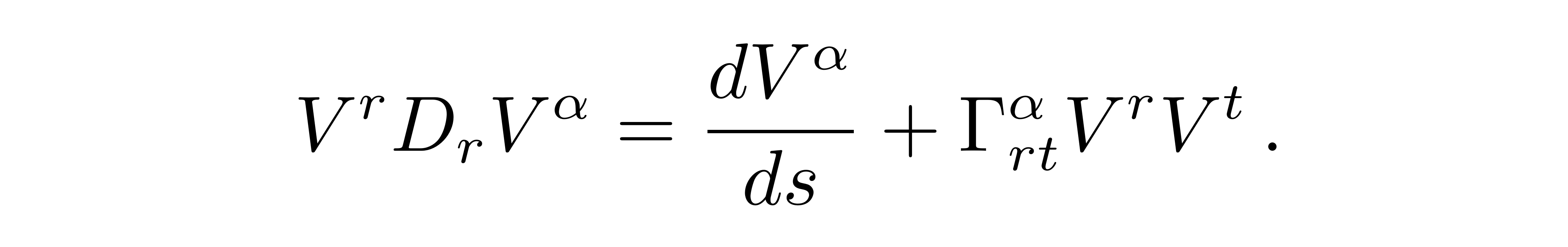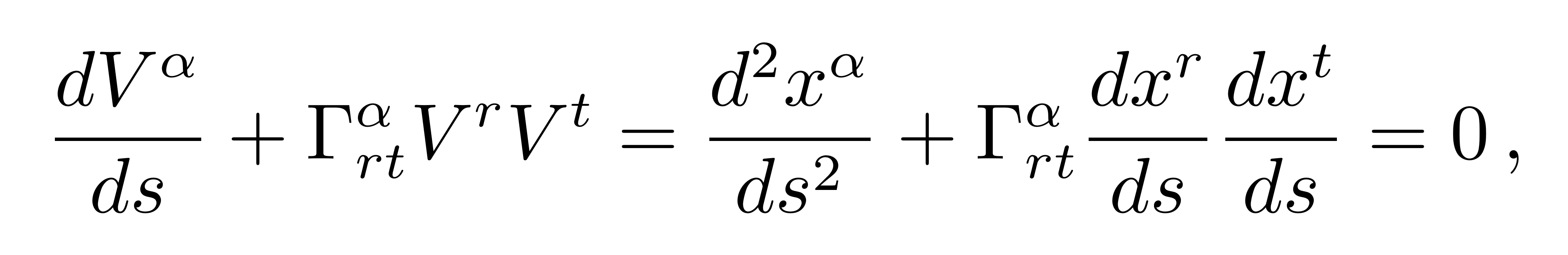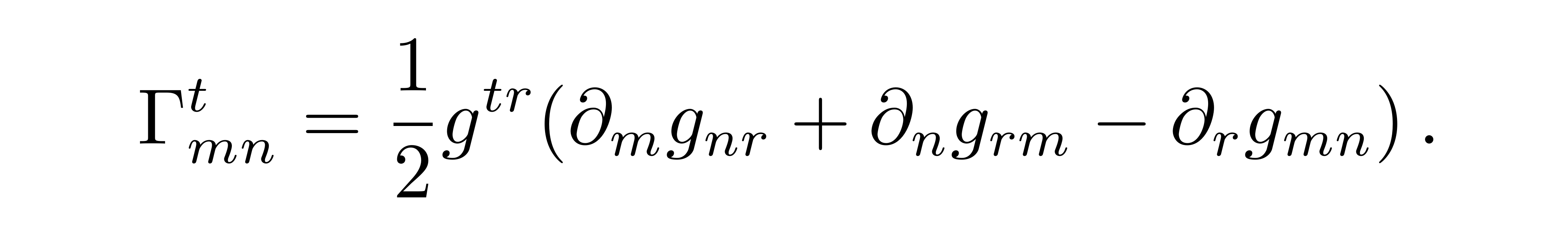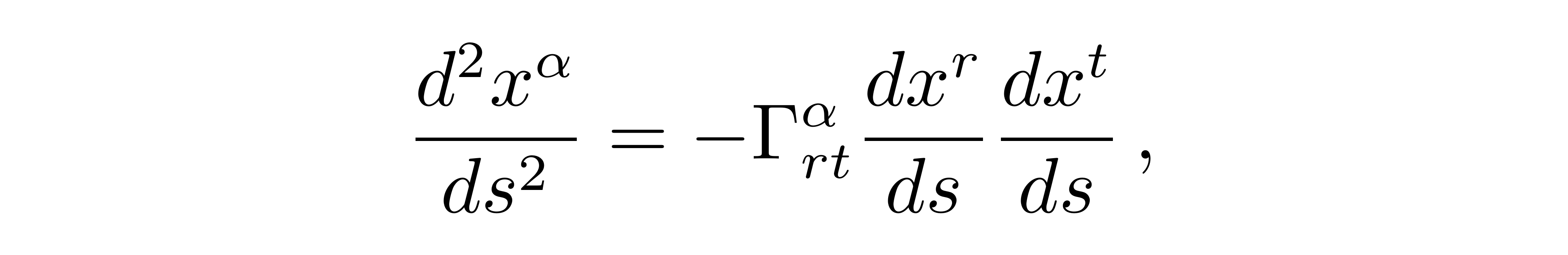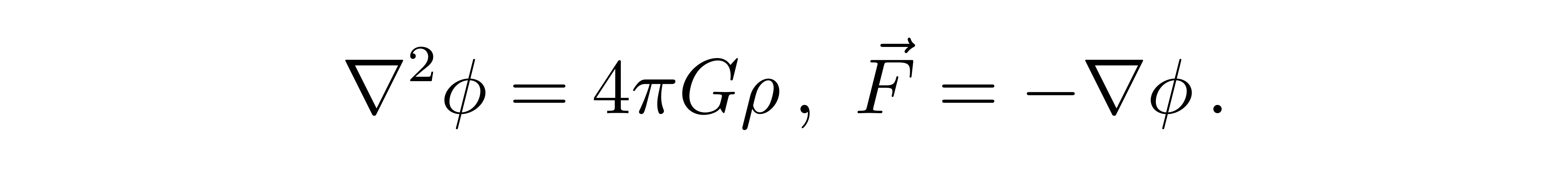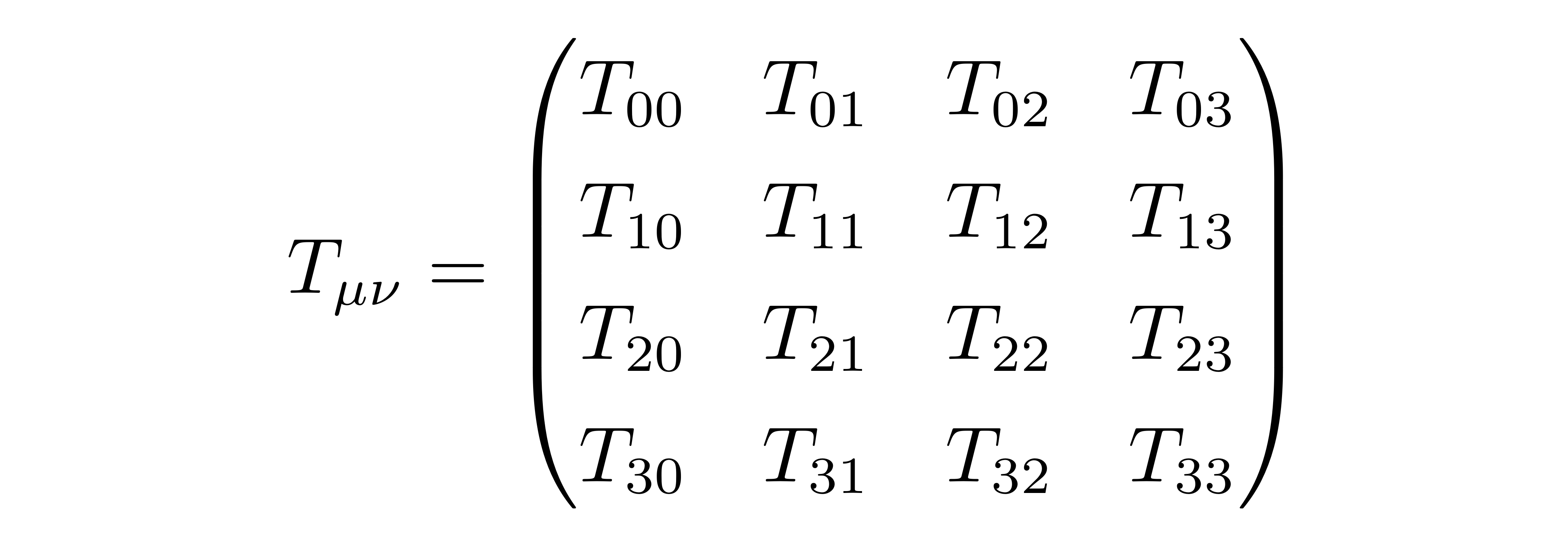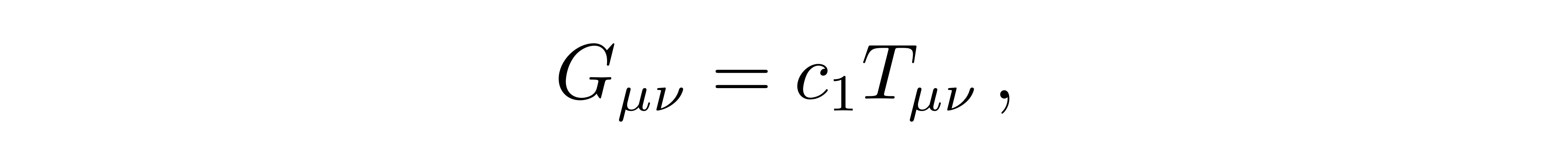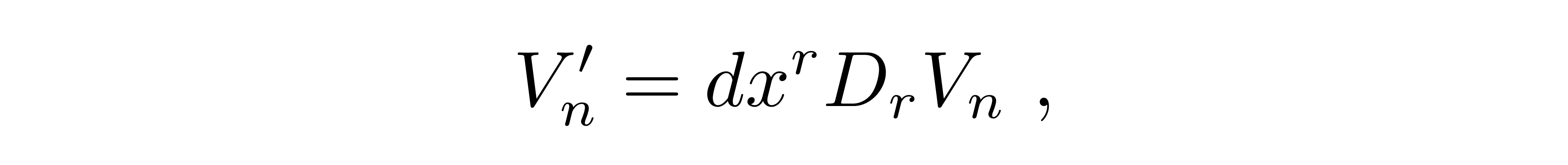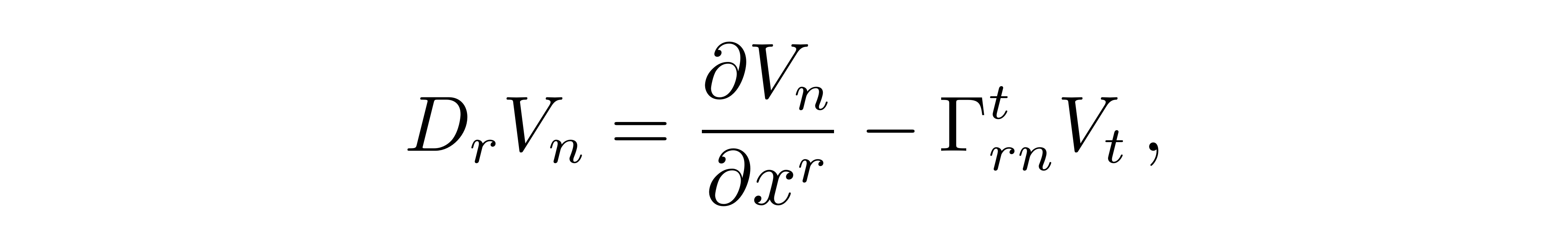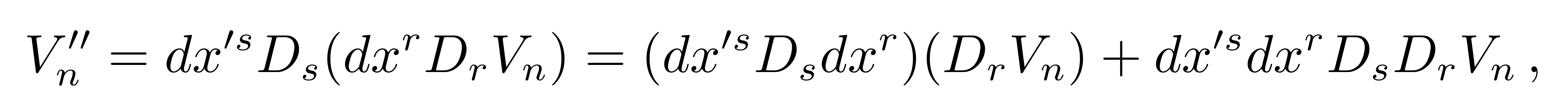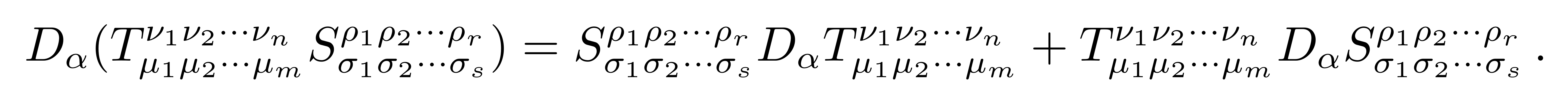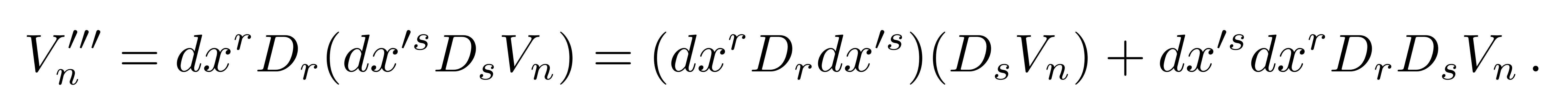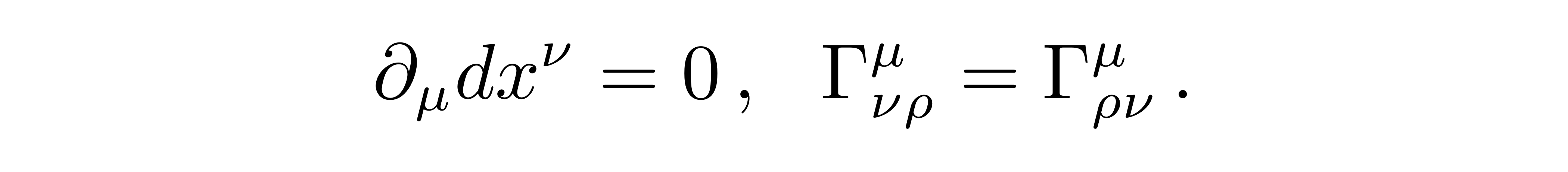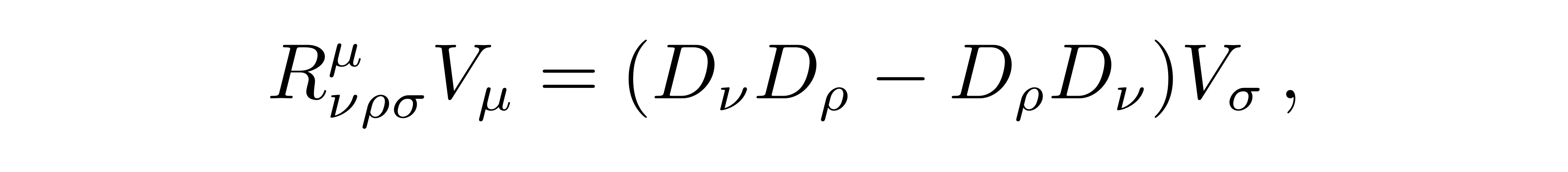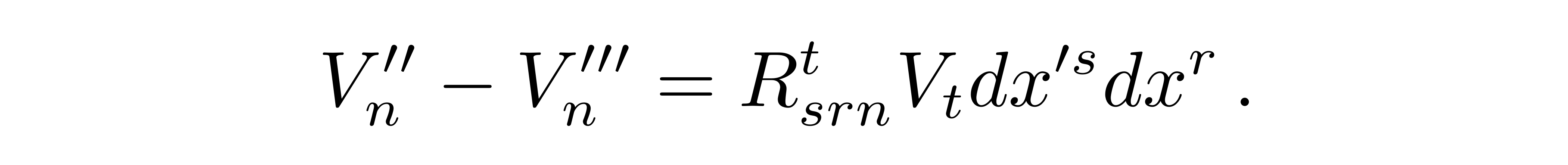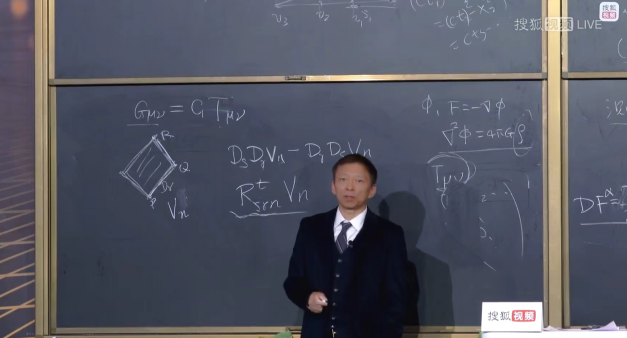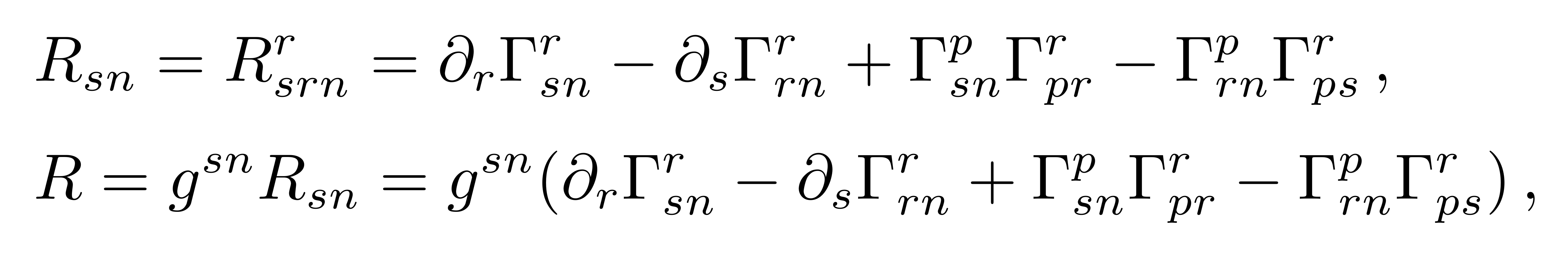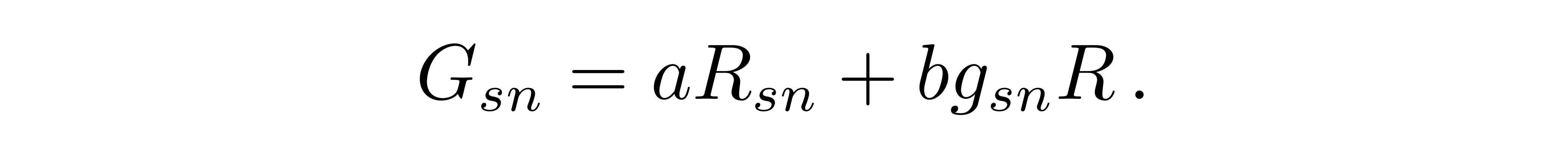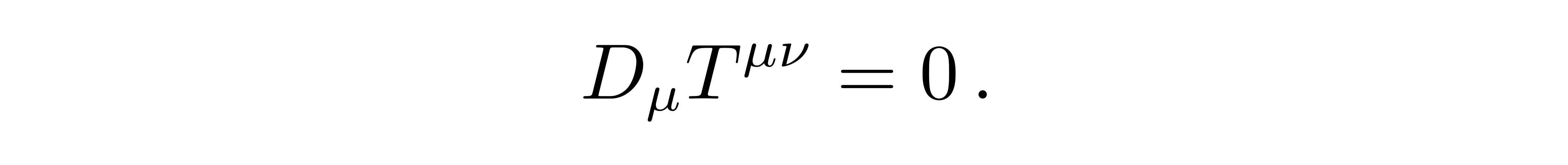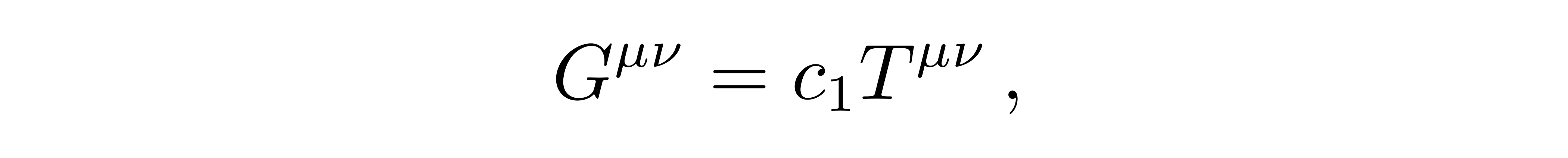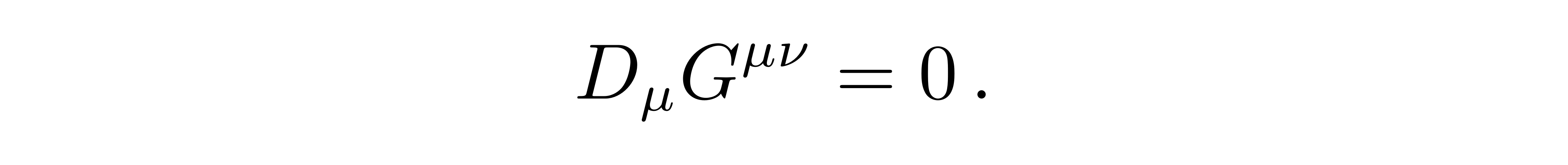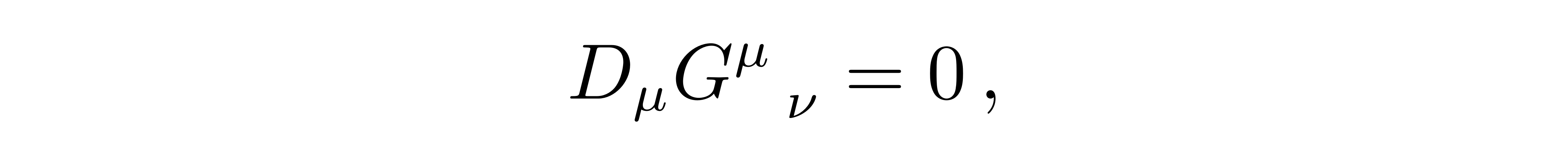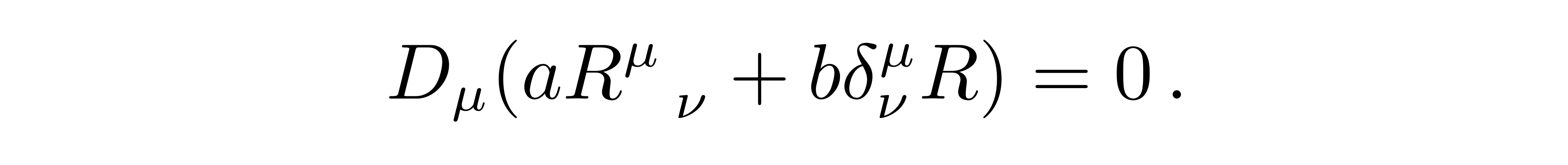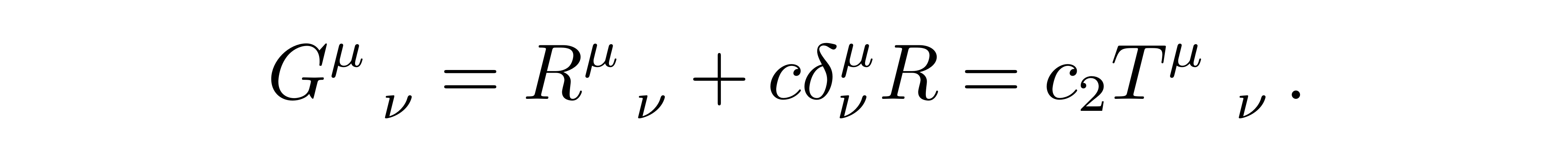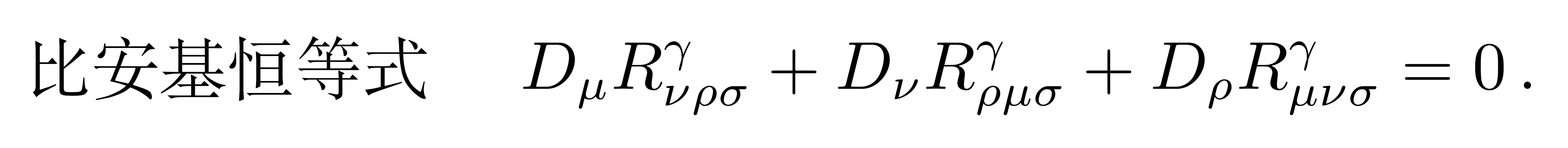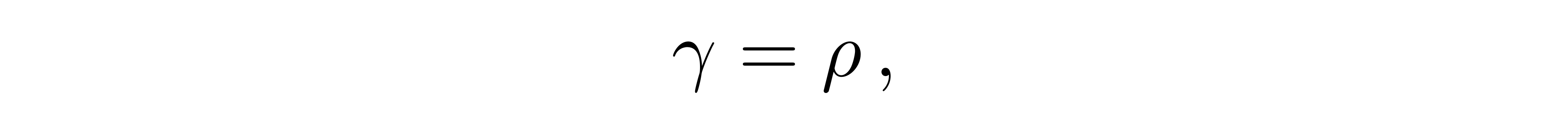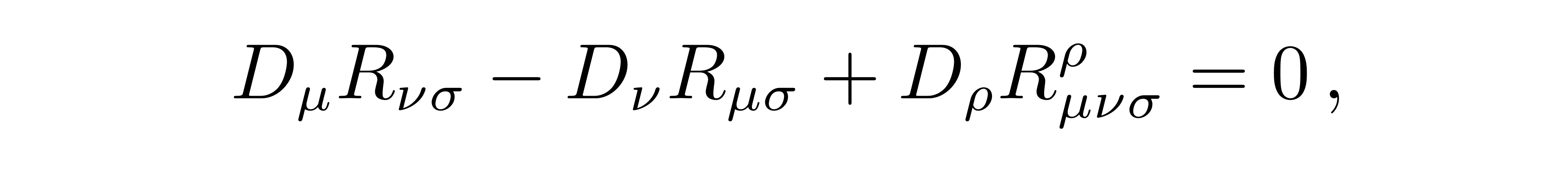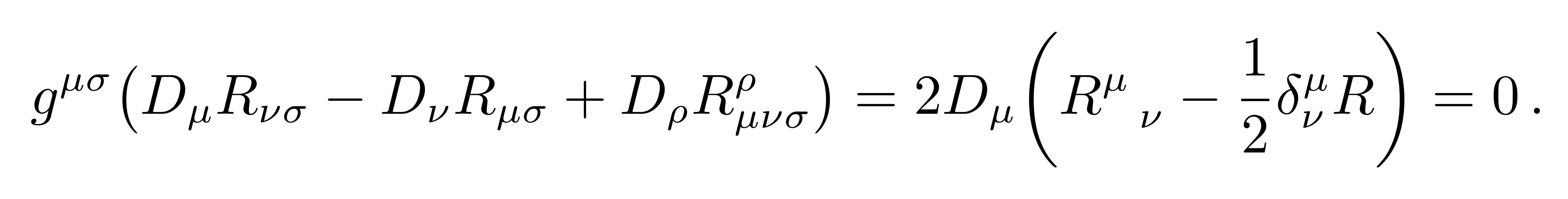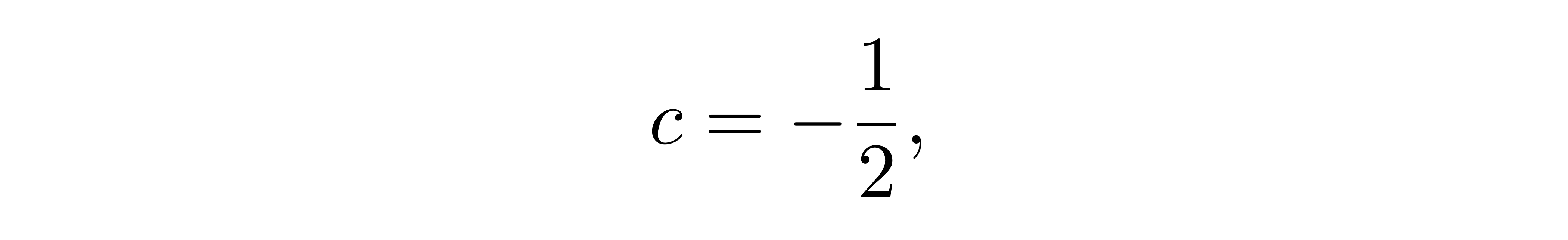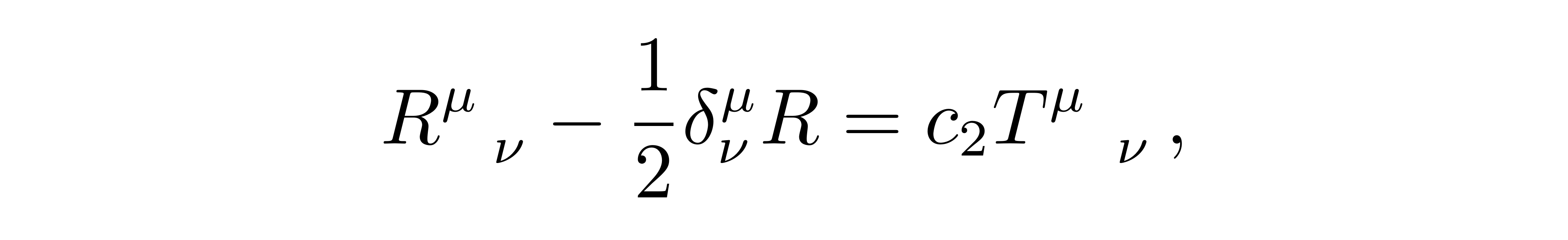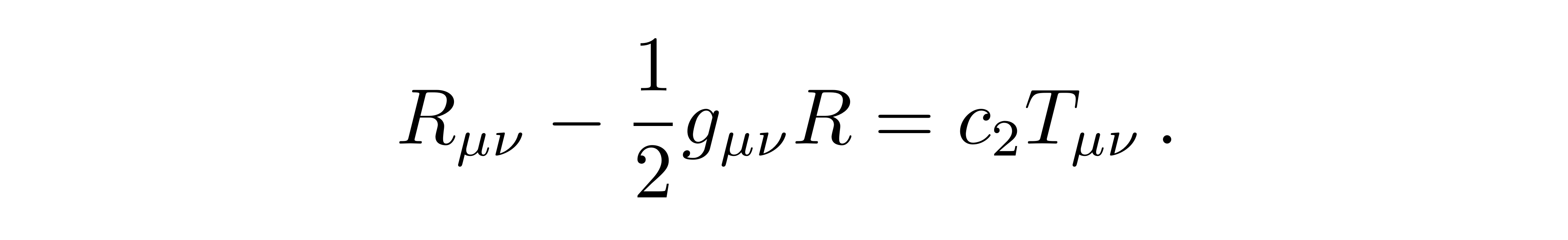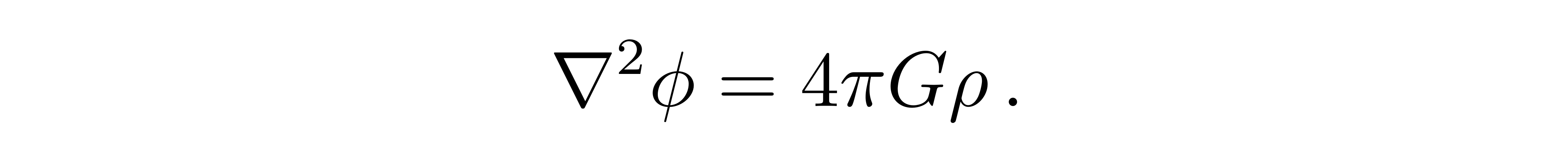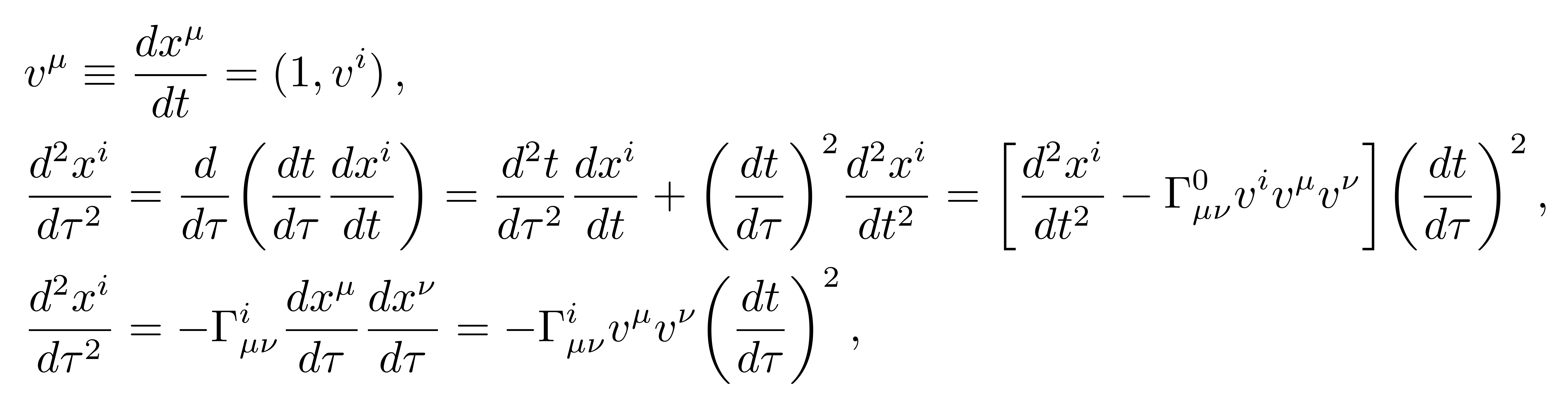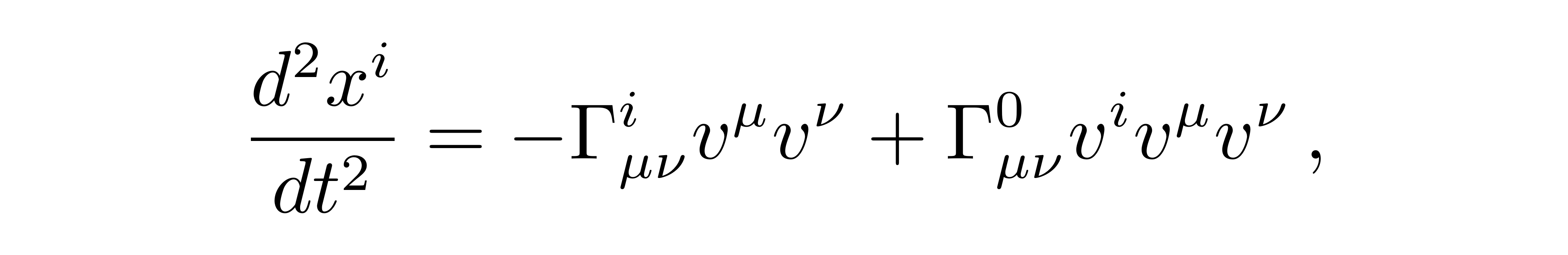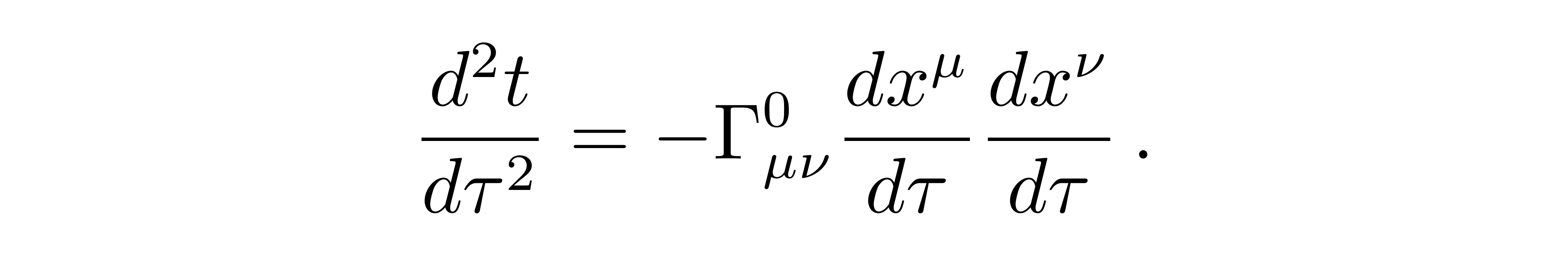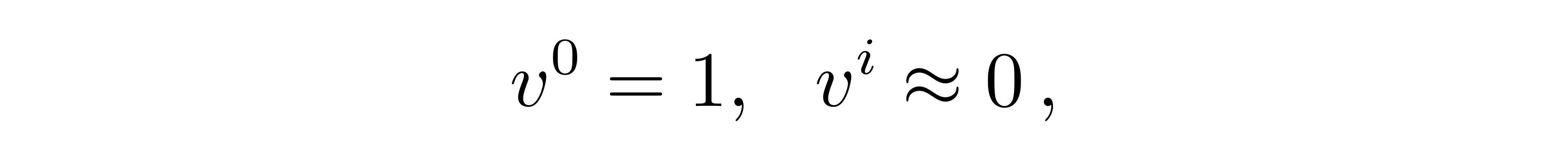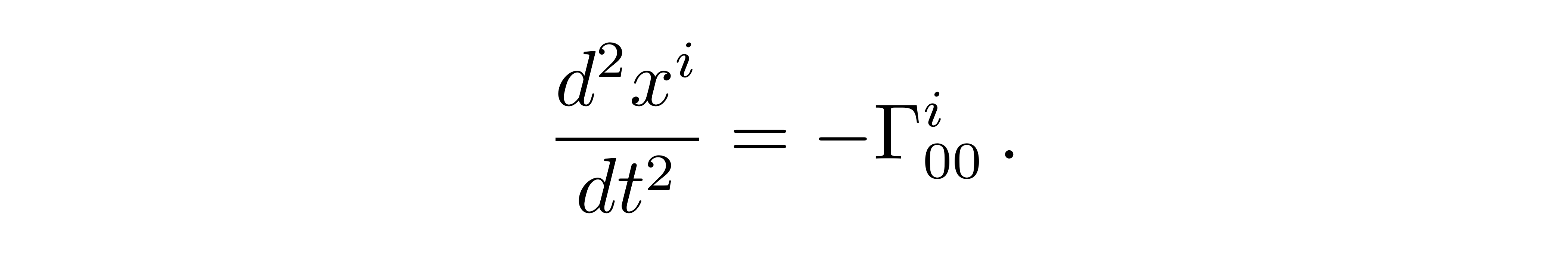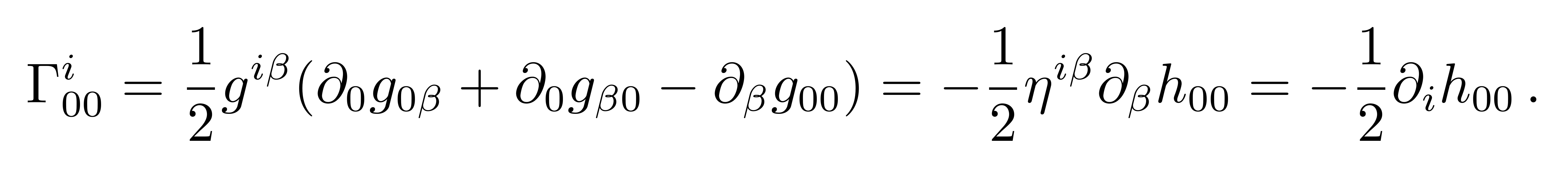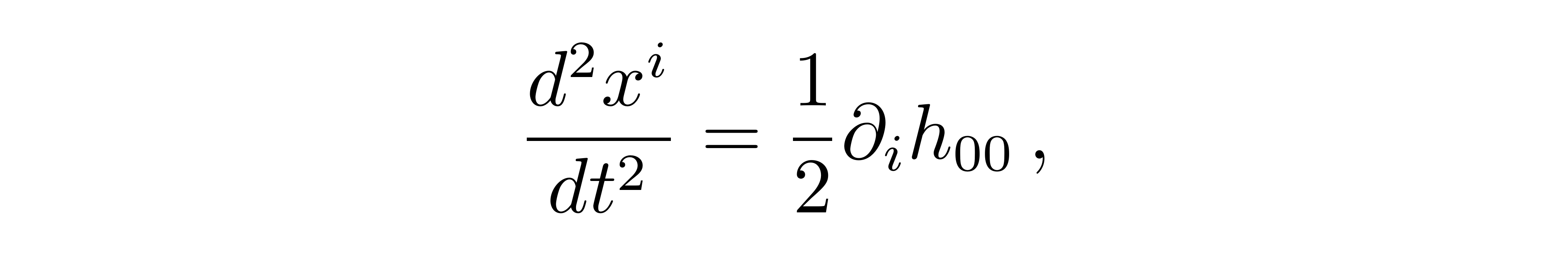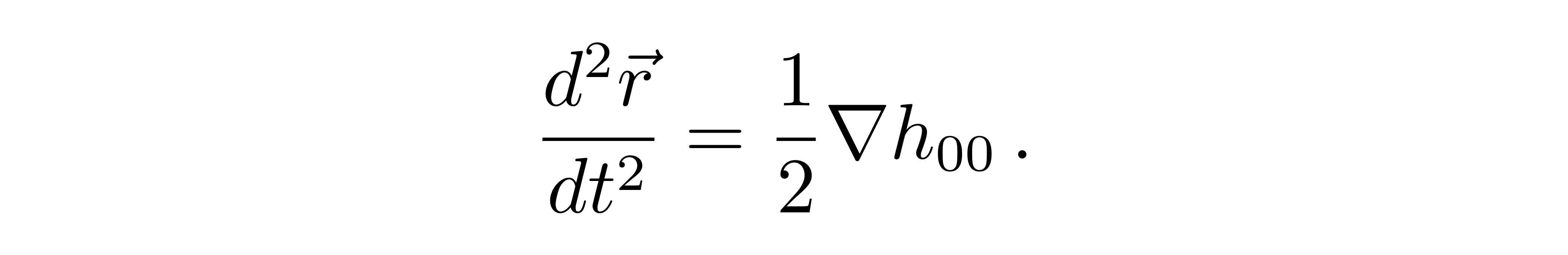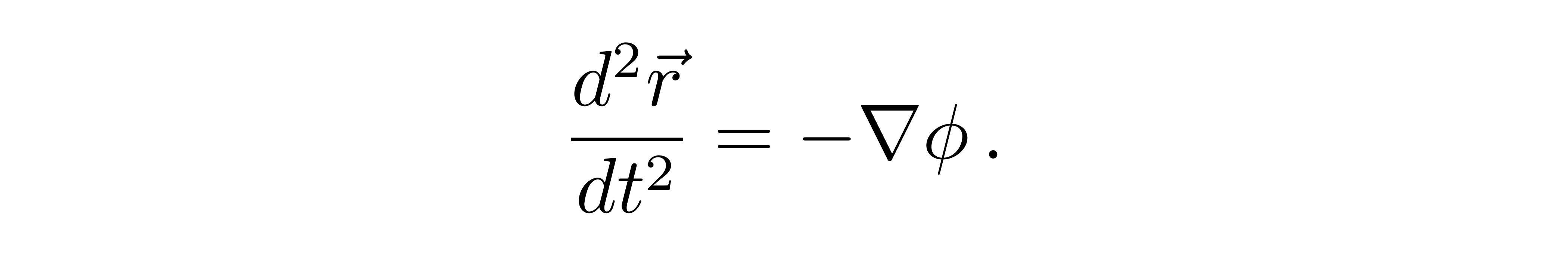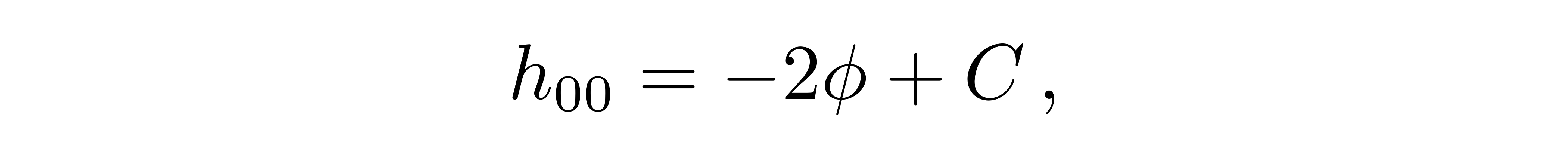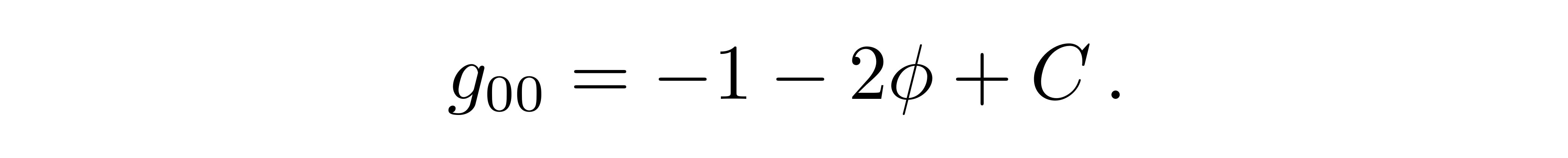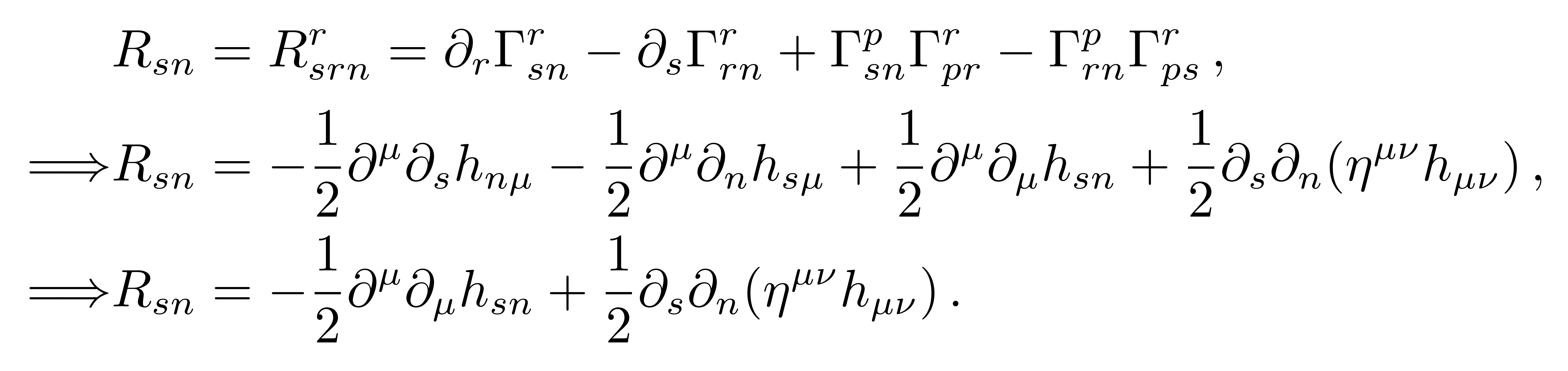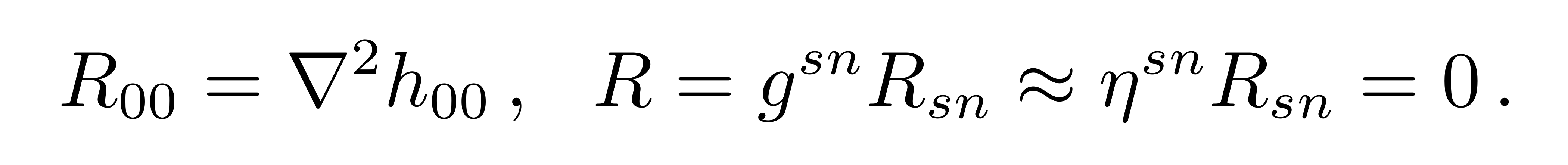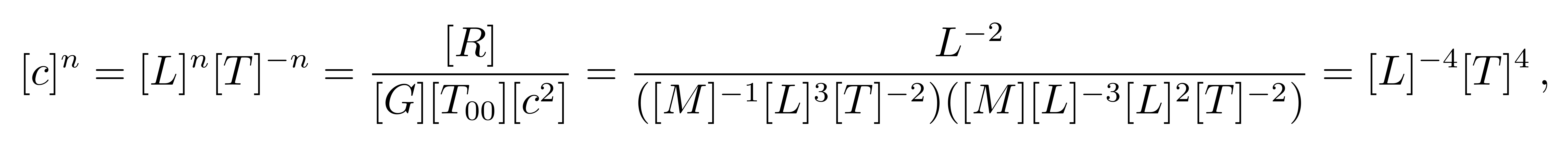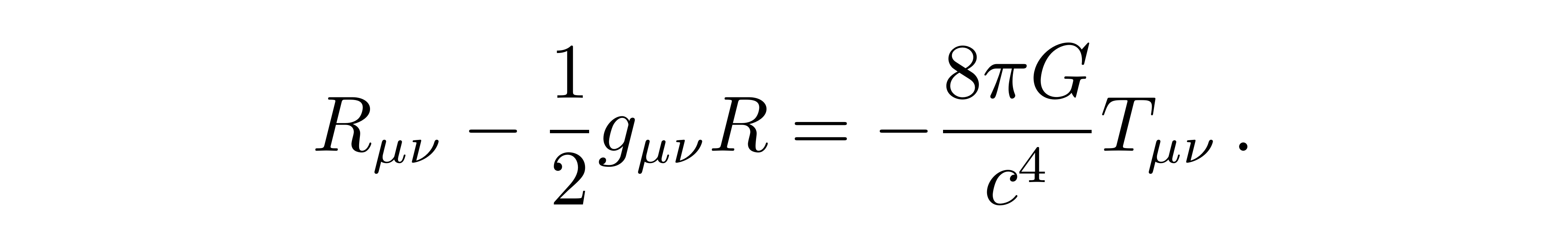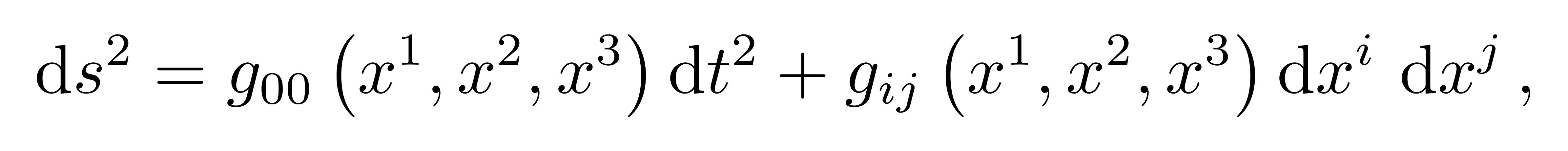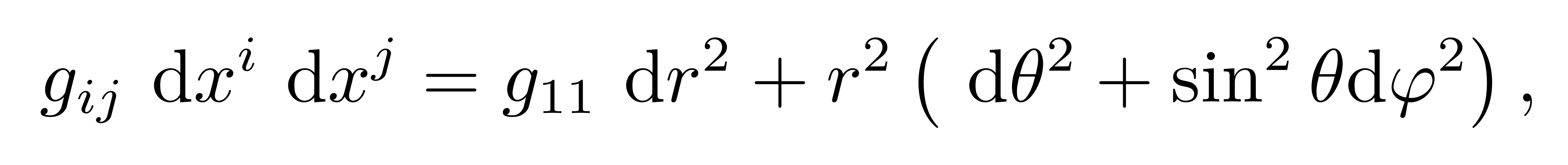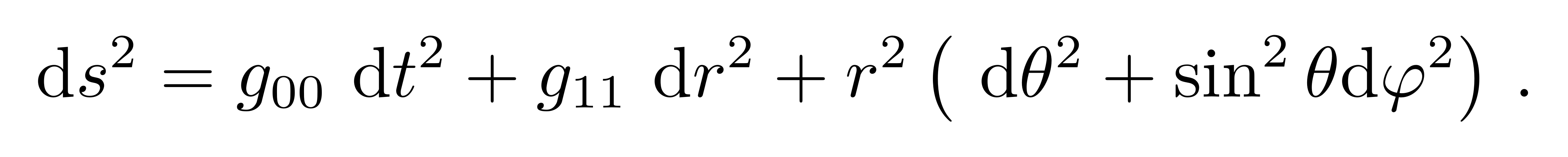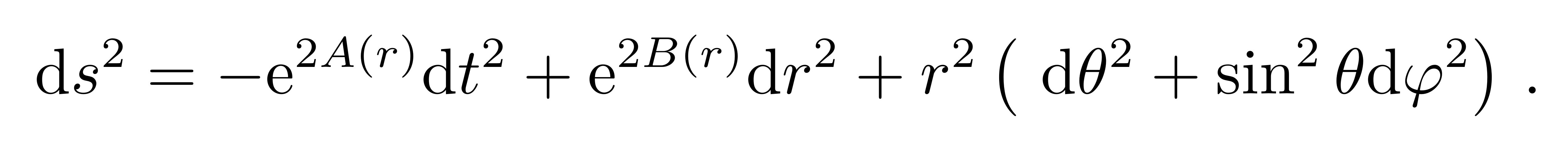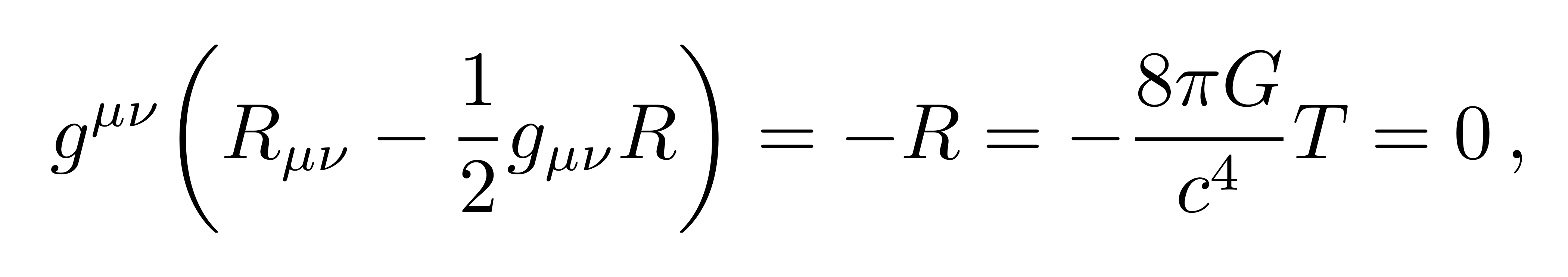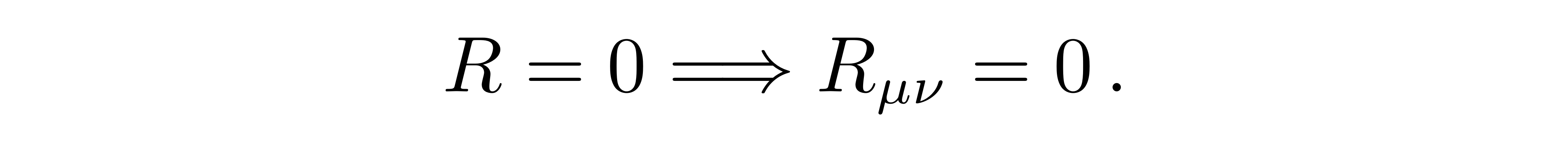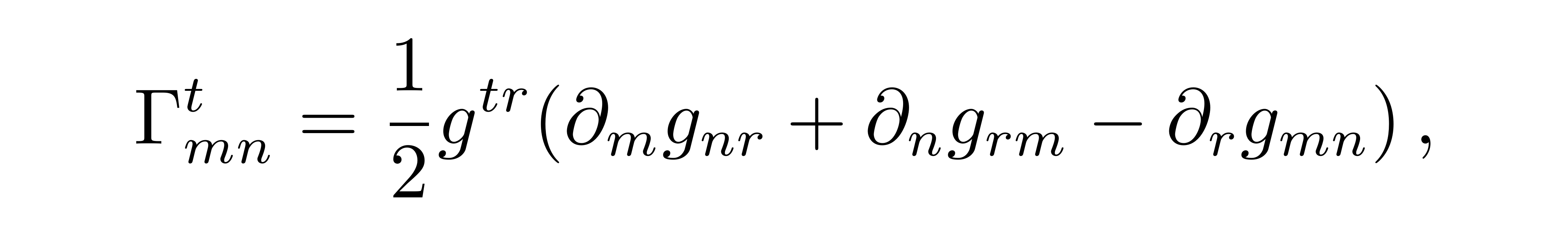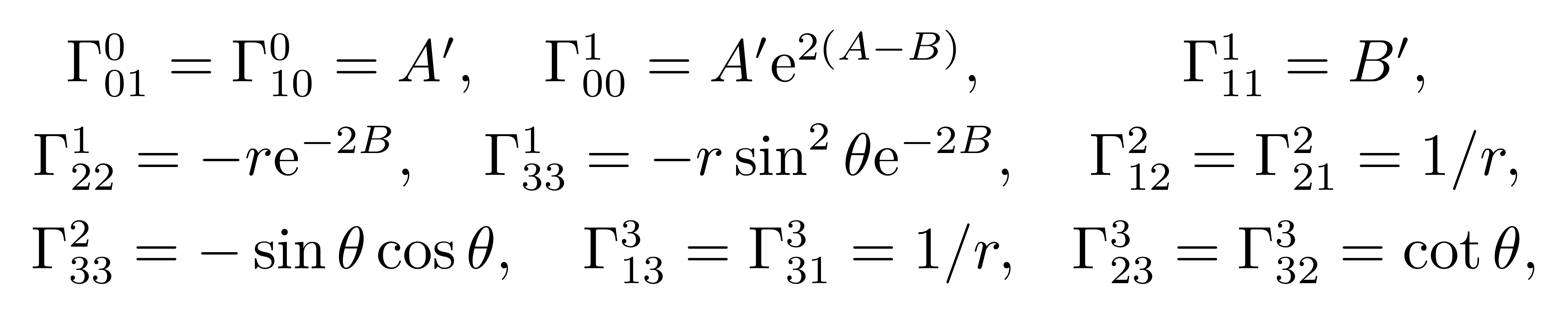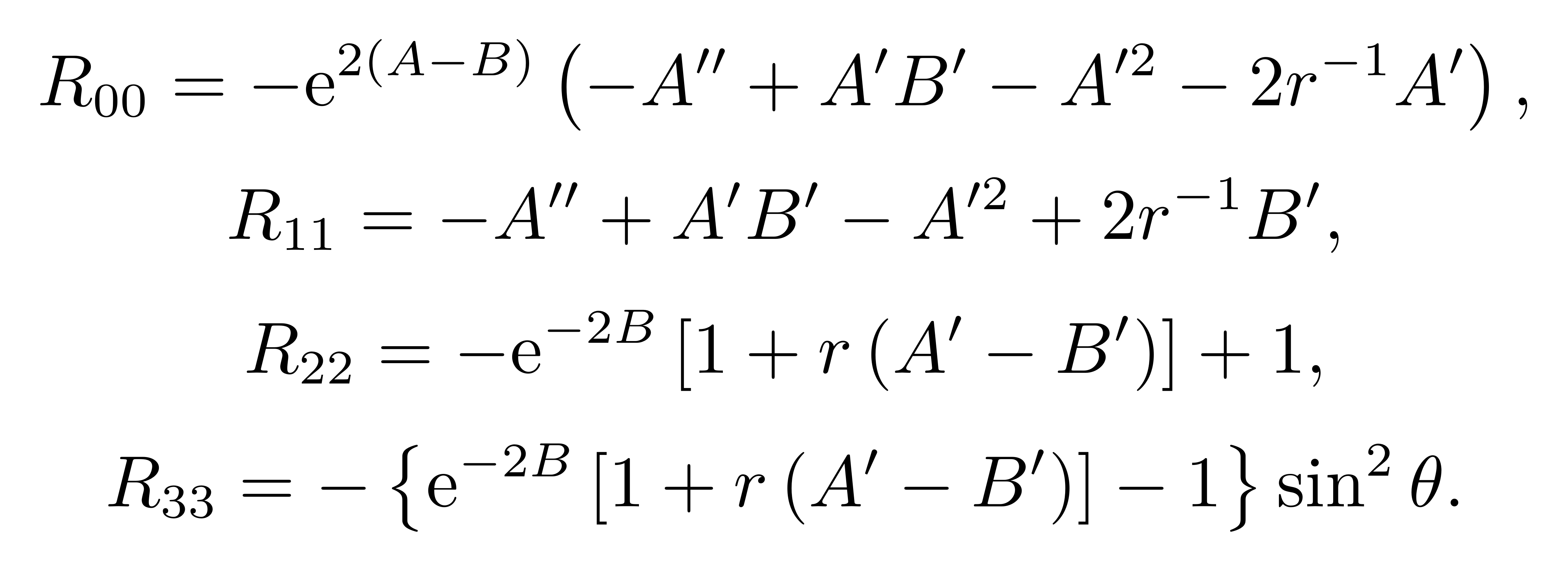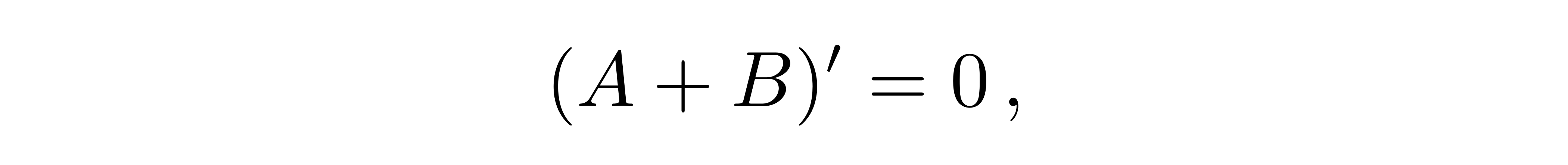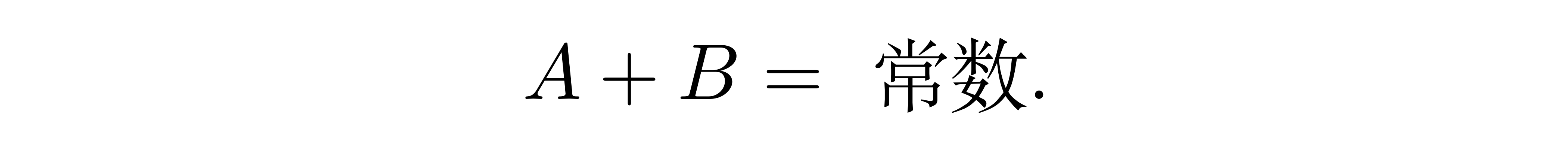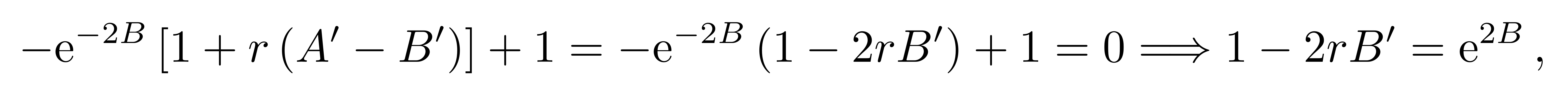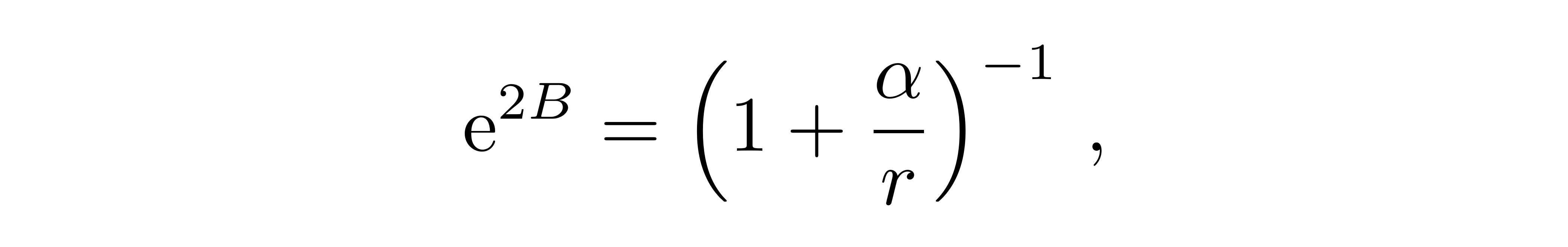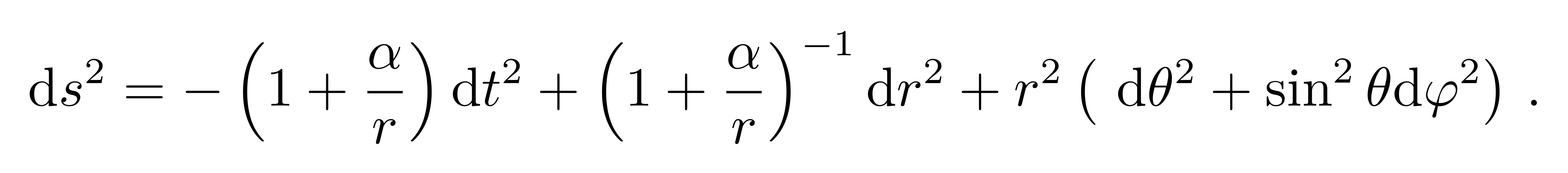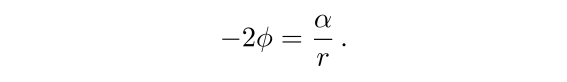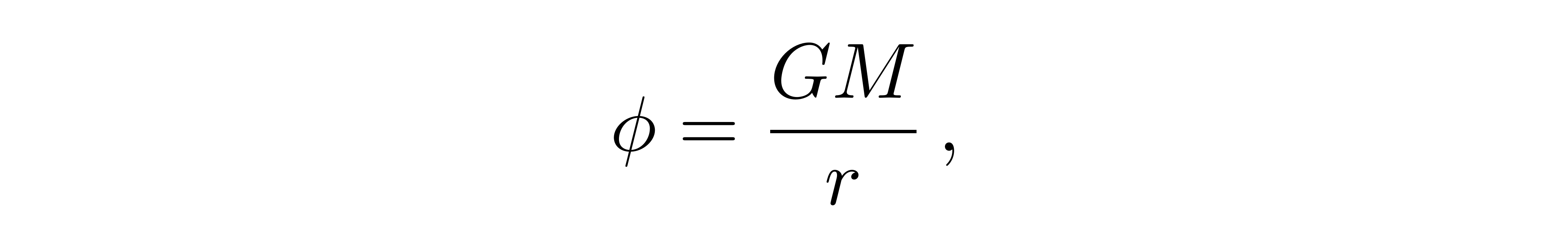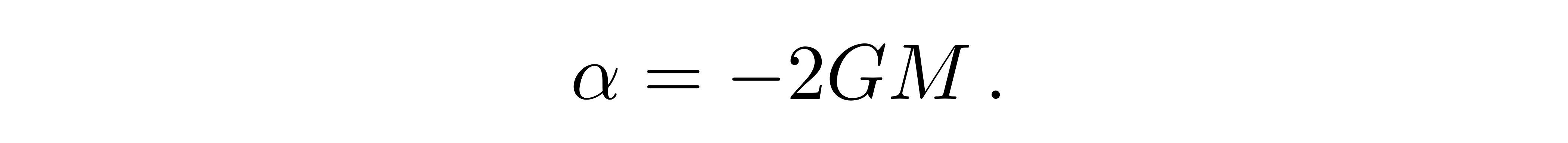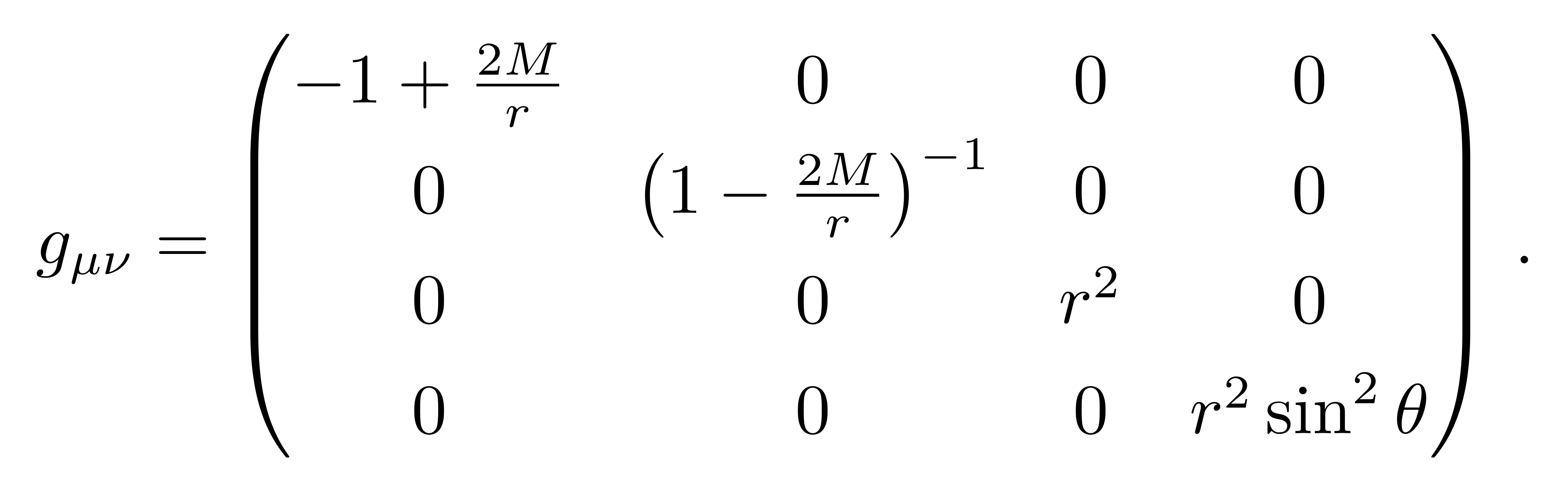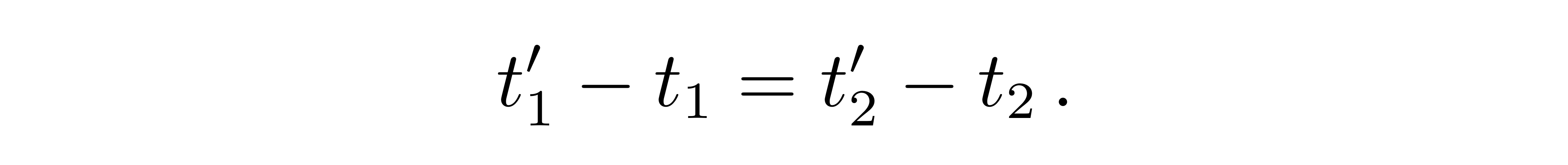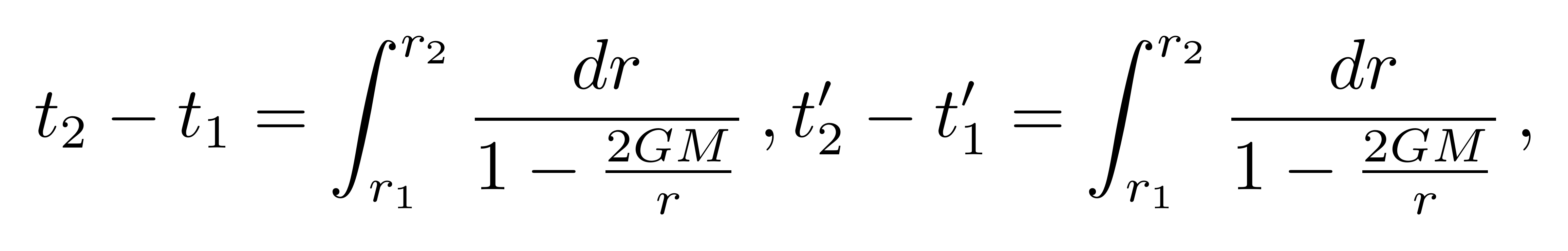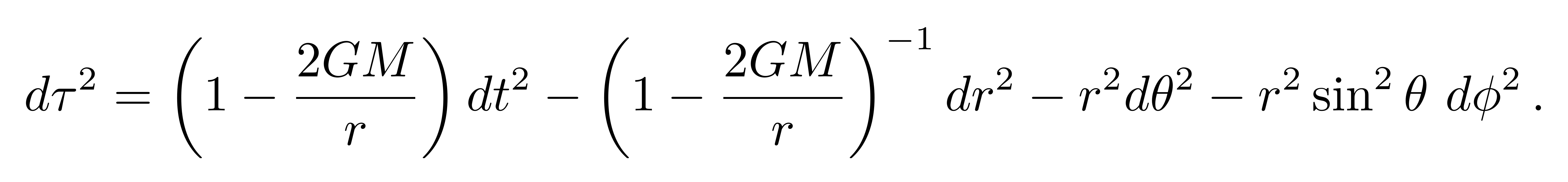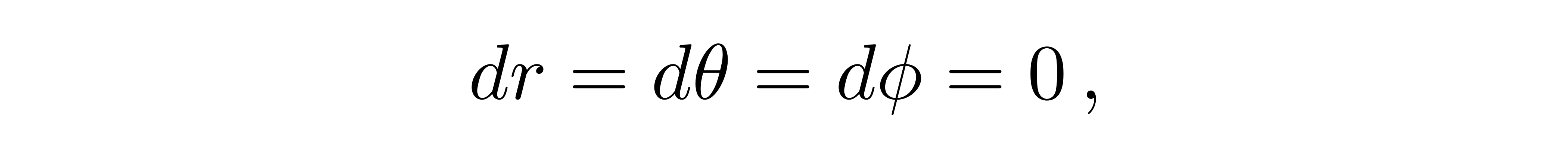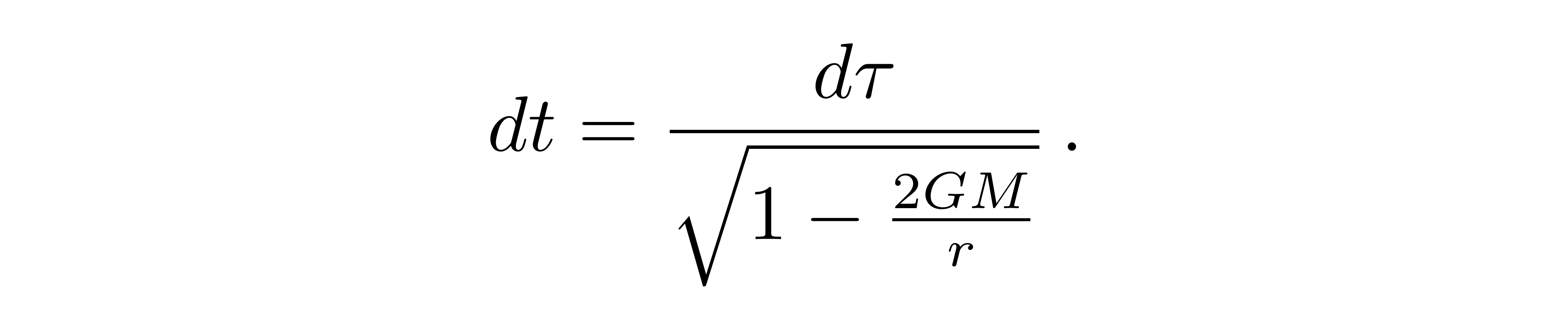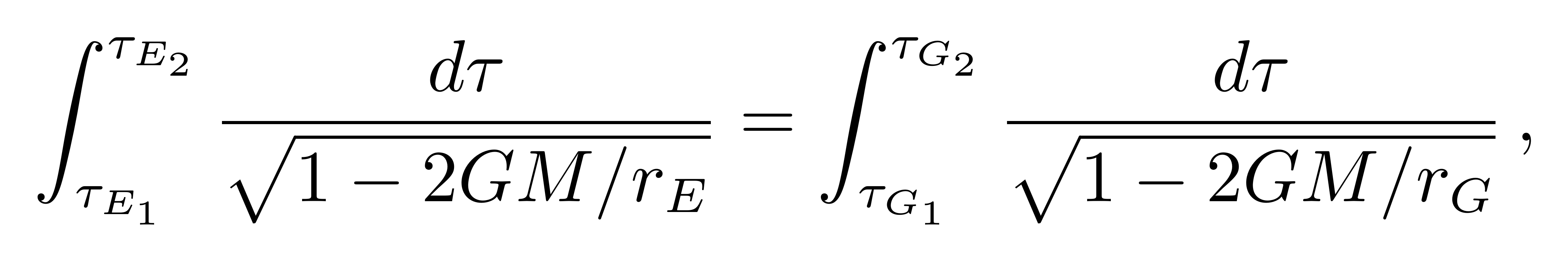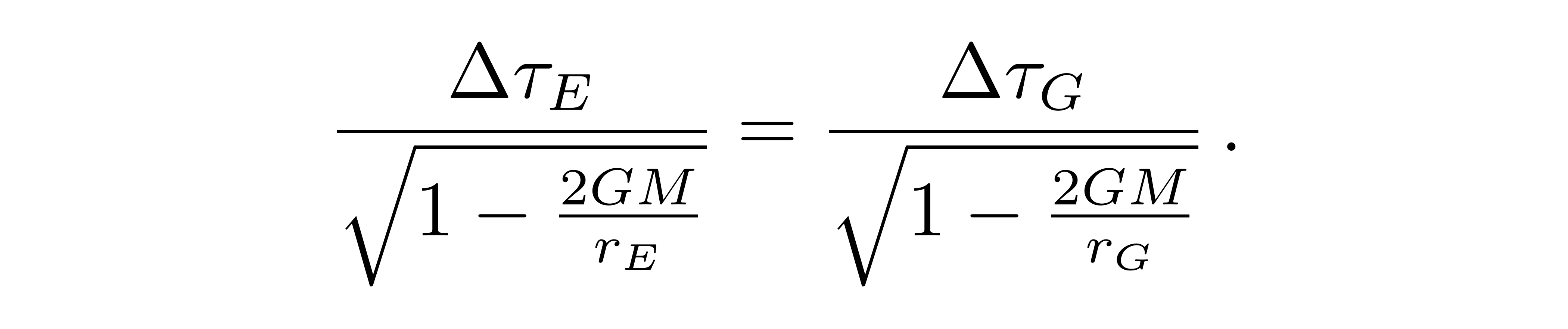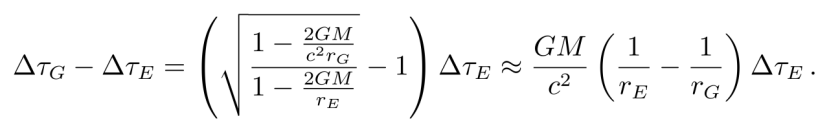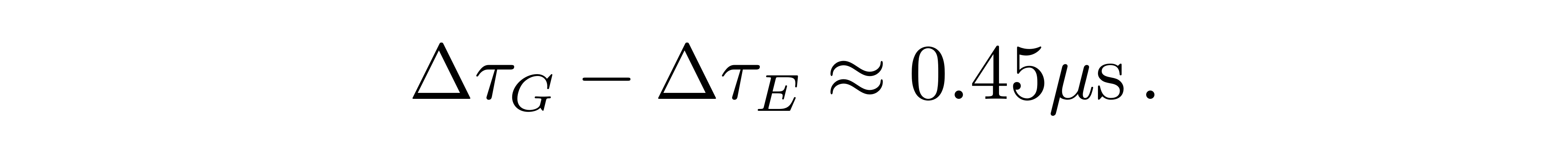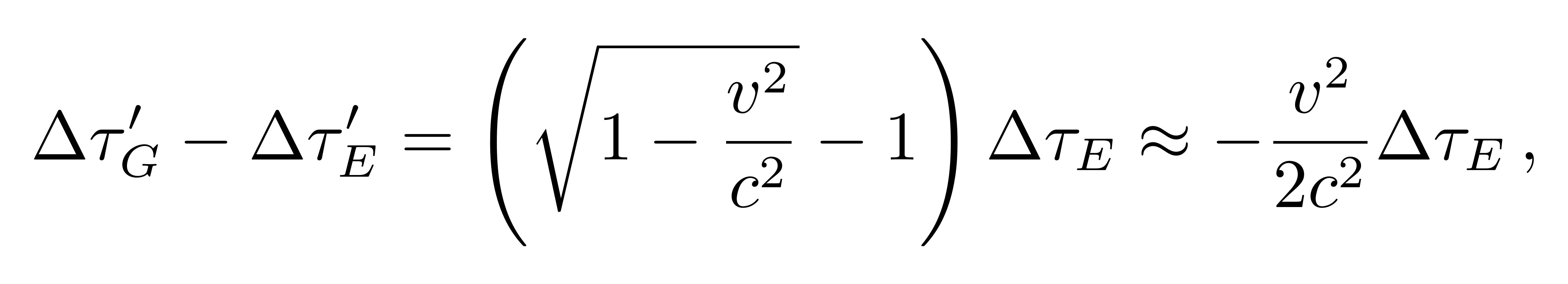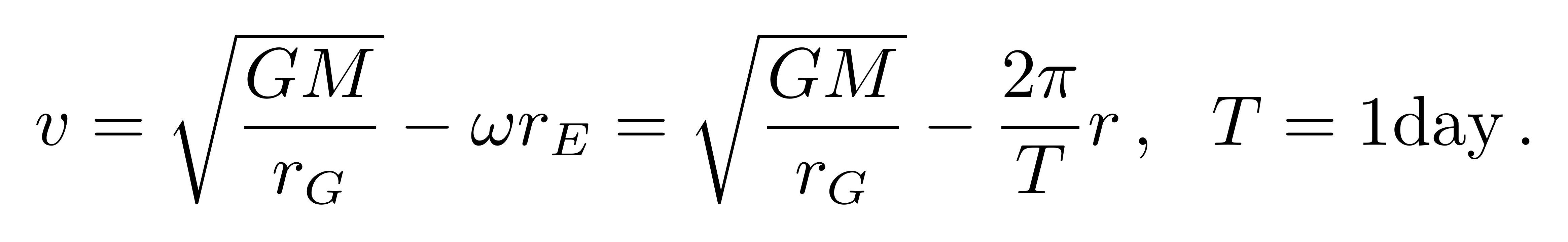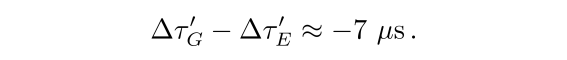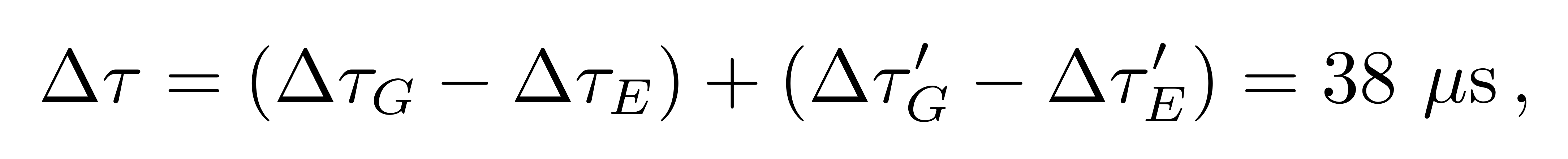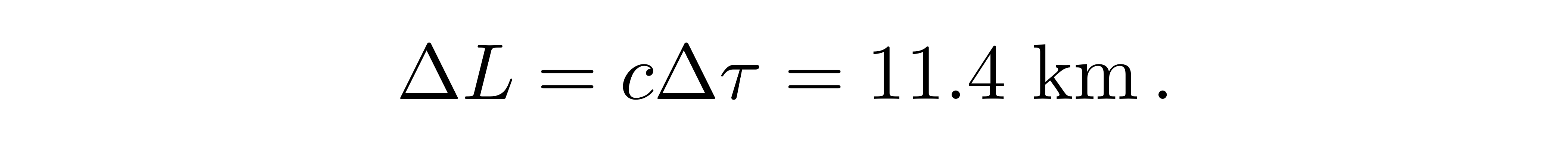The software will be deployed in all fitness facilities of the 9Round brand under Aqtab in the Kingdom of Saudi Arabia, United Arab Emirates, Kuwait, Bahrain and Oman.
To further improve the user experience of our tools, in close cooperation with 9Round Fitness, Perfect Gym will translate and adapt all required products into Arabic.
20 Real Ways to Make Money From Home for Free in 2023
Upwork
ocean casino online Top betting sites will let you withdraw funds at any time.
Here are the most popular questions we get asked about ways to place a bet:
2023年12月31日,搜狐创始人、董事局主席兼首席执行官、物理学博士张朝阳举行跨年演讲,跟大家一起学习广义相对论,加深对时间的理解。张朝阳首先回顾了狭义相对论,考虑加速观者所看到的世界,接着类比三维空间中的直线,强调了弯曲时空中的测地线和等效原理。
而后,张朝阳详细地推导并讲解了黎曼曲率张量的含义。紧接着,张朝阳根据能动张量的守恒性质和比安基恒等式(Bianchi identities),给出了爱因斯坦张量,并假设爱因斯坦张量正比于能动张量。在弱场近似的条件下,张朝阳比较了测地线方程和牛顿引力下的泊松方程,获得了爱因斯坦张量与能动张量的比例系数,通过量纲分析完整地推导出了爱因斯坦场方程。然后,张朝阳计算了著名的史瓦西时空解。最后,根据史瓦西解,张朝阳计算了GPS卫星每天的定位误差。
 (张朝阳讲解爱因斯坦场方程)
(张朝阳讲解爱因斯坦场方程)
狭义相对论回顾
要理解广义相对论则离不开始于狭义相对论的时空观。时间和空间并非独立的而是一个整体。在整个时空里我们只关心只有洛伦兹变换下协变的量,其中最重要的不变量就是时空中的度规或者等价的线元,即时空间隔。如何理解时空间隔以及相应的洛伦兹变换,可从欧氏空间的转动作为类比开始研究。
假设在二维欧氏空间中有一个矢量R,其在原坐标系中的坐标是(x,y),与x轴的夹角为θ,
![]()
现将坐标系旋转角度φ,经过这个旋转变换得到矢量R的另一个坐标
![]()
新旧坐标之间的关系为
![]()
可以看出,欧氏空间中一个矢量在转动变换下是不变量。类似地,时空中的洛伦兹变换也是某种转动,称为伪转动。我们仍以2维为例,不同之处在于其中的一维是时间。此时表示不变量的时空间隔可用双曲三角函数展开
![]()
对这样一个量做坐标变换为
![]()
其中
![]()
我们最终得到如下关系
![]()
![]() (张朝阳讲述洛伦兹变换)
(张朝阳讲述洛伦兹变换)
这就是洛伦兹变换,在闵氏时空中起到类似于转动的作用。闵氏时空的线元写为
![]()
或者用更整齐的二次型表示
![]()
其中
![]()
称作闵氏度规。
加速参考系和Rindler时空
我们用(T,X,Y,Z)表示一个惯性坐标系,用(t, x , y, z)表示匀加速坐标系。存在一个如下的坐标变换联系两个坐标系
![]()
其逆变换为
![]()
若x为一常数,可看出此逆变换在惯性系中描述的就是一条双曲线。进一步让x变化,就可以用无数条互不相交的双曲线将惯性系所描述的 -X<T<X的区域覆盖。我们对上述正变换求微分,得到
![]()
将之代入闵氏时空的线元中
![]()
即可获得匀加速系下的线元表达式
![]()
上述的坐标变换只有在区域
![]()
上成立,这一块区域被称为Rindler楔形(Rindler wedge)。从上面的Rindler坐标下的线元可以看出,一个粒子在时空中运动若满足在空间位置处的下述条件
![]()
则此世界线的原时与加速系的时间等价
![]()
在各个不同的x和y点的所有做不同匀加速运动的粒子,可将Rindler楔形填满。如果换成快度(rapdity)φ和x'来表述,有
![]()
![]()
![]() (张朝阳讲解加速系看闵氏时空)
(张朝阳讲解加速系看闵氏时空)
从线元
![]()
中我们就可以看到加速系看到的闵氏时空似乎存在着某种“弯曲”。这为爱因斯坦在后面创立广义相对论提供了一些线索和端倪。
等效原理与测地线方程
张朝阳说,任意一时空,从局部来看,都与闵氏时空无法区分,或者可以说,时空可以被看作是由一个个闵氏时空拼接而成的。在这个时空中,所有物质都不再以占据一定空间体积的存在方式存在,而是被描述为一条世界线,其中每一点代表物体在空间中的位置延伸。爱因斯坦在狭义相对论发表后,开始思考如何描述加速观者,也就是非惯性观者的世界线。同时,他也对引力质量和惯性质量相等的现象感到困惑。
张朝阳紧接着说到,我们知道,带电物体之间会产生库仑力,而库仑力的大小与电荷量成正比,与物体质量无关。然而,万有引力不同,它的“荷”实际上就是物体的惯性质量。这启发了爱因斯坦思考:究竟是不是真的存在一种叫做引力的“力”?或许引力只是与物体惯性相关的某种“惯性力”?另外,加速运动中的物体看到的世界与惯性观察者看到的世界是不同的,仿佛时空发生了一种“扭曲”。例如,坐在自由下落电梯中的观察者只感受到引力的影响,几乎无法区分他所经历的是某种惯性力还是万有引力。因此,爱因斯坦大胆地猜测:引力可能并不是真正的力量,而是由于时空的弯曲所产生的某种惯性效应。这里需要强调的是,只有当存在引力相互作用时,时空才会真正发生弯曲。时空的弯曲是绝对的,不依赖于观察者的角度。
在弯曲时空的概念中,引力不再被视为一种力量,而是一种几何效应。因此,需深入研究时空弯曲的微分几何性质。张朝阳通过一个生动的白纸示例引入了平直空间的概念。他指出,即使在从三维空间到二维圆柱面的情况下,空间仍然可以保持平直性,这意味着两条平行线在此仍然不会相交,并且勾股定理和三角形内角和等于180度的规则仍然适用。然而,当我们考虑到球面这种存在曲率的情况时,情况发生了变化,三角形的内角和不再等于180度,而且两条平行线在球面上会相交。因此,我们需要将平直空间的一些概念和定义推广到弯曲的时空中。
但是到目前我们仍然不清楚引力和惯性之间是如何对应的。而爱因斯坦继续思考,平直时空中做惯性运动的观者走的是直线,既然引力不过是让时空弯曲,那么只要找到弯曲时空中的“直线”,惯性观者仍然走这样的“直线”就行了。所以我们需要将平直时空中的直线的概念推广到弯曲时空中,这就是测地线的概念。张朝阳以一趟从北京飞往纽约的飞行为例进行了说明。他解释了飞机选择的航线,该航线经过北极上空,穿过安卡拉等城市,这条路径实际上是两个城市之间的最短路径,它是大圆的一部分。在三维平直空间中,我们可以将直线视为一个矢量沿着自身平移而形成的路径。
在三维平直的空间中,一个矢量 F
![]()
沿着一条曲线平移,其变化为
![]()
其中这条曲线的线长参数为s。如果我们让这里的F就是矢量v本身,并且这一改变量为0,根据上面提到的直线的定义,这就是一条直线:
![]()
其中我们用到了V的切矢表达式
![]()
这里的坐标x的解是
![]()
其中x0和v0是常数,这就表示一条三维平直空间中的一条直线。但在非平直空间的曲面坐标系中,在平移的时候标架也会改变,我们须把这种沿着曲线平移的改变量写为
![]()
其中的克氏符就是表示为标架改变的一个效应:
![]()
因此在弯曲时空中,将普通导数推广成了上述的协变导数。我们现在认为矢量F是曲线的切矢,后面记为V,它沿着自己的积分曲线平移,其中线长参数为s,则方程可以重写为
![]()
若此方程等于0,则定义了测地线方程,也就是弯曲时空中的直线:
![]()
其中克氏符可以用度规张量表达
![]()
将方程重写为
![]()
则可以重新理解牛顿的万有引力,引力产生的加速度实际上就是几何效应,由时空弯曲带来的。
![]() (张朝阳介绍测地线方程)
(张朝阳介绍测地线方程)
爱因斯坦场方程
理解了测试粒子在时空弯曲中走起来会出现一个看起来的非零加速度后,我们就应该思考时空如何被物质所弯曲,也就是引力的源头怎么来描述的。张朝阳提醒到思考这个问题的线索可从牛顿引力的泊松方程和力出发
![]()
从这两个方程出发,可以想像,力会导致动量密度流的传递,同时一个方向动量密度的改变可能导致另外两个方向的动量密度的改变,即产生压强,这些情况都会让引力势发生改变,但是这些效应都不能从泊松方程中体现出来,所以用能量密度这一个标量描述引力似乎自由度还不够。从这些可能性去构造物质部分,我们可以直接给出一个二阶的能量动量张量去描述物质
![]()
这里的00分量表示物质的能量密度ρ,0i分量表示沿空间i方向上的能流密度,ij分量代表动量密度的i分量在j方向上的变化率。因此可以猜测场方程的形式应该是
![]()
其中c1是一个比例系数,左边应是描述时空弯曲的二阶张量。
时空的弯曲可以用曲率描述,我们下面再看一下曲率的意义。一个协变矢量V在一个空间中沿着一条方向为r的曲线从P平移到Q点,假设这一段很小,则相当于坐标做了如下变化
![]()
即坐标的变化量为dx。因此平移到Q点处的矢量V'变成为
![]()
而其中协变导数为
![]()
这里的第一项是一个普通导数,第二项可理解为由于基矢变化而导致的矢量V的变化。此二阶张量DV的分量可表示为一个4x4的矩阵。如果矢量V'再沿着方向为s的曲线从Q点平移到R点,仍旧假设这一段路径很小,则相当于坐标又做了如下变化
![]()
即坐标的变化量为dx'。类似地,平移到S点处的矢量V''变成为
![]()
其中我们用到了协变导数的线性性
![]()
现在我们类似地让矢量V平移两次,但先沿着方向为s的曲线平移dx'到达Q1点,再沿着方向为r的曲线平移dx到达R点,则新的矢量V''' 为
![]()
接着我们把这两个矢量V''和V'''相减得到
![]()
其中用到了对坐标基矢的普通导数等于0的条件以及克氏符的对称性
![]()
因此我们可定义黎曼曲率张量R为
![]()
使得两种平移所得的矢量V''和V'''与原先的矢量V有如下线性关系
![]()
黎曼曲率张量的定义说明,一个矢量的二阶协变导数交换次序后产生的三阶张量,等于一个四阶的张量与矢量自身的缩并。根据黎曼曲率张量的定义,可将协变导数表示为普通导数和克氏符的组合
![]()
![]() (张朝阳介绍黎曼曲率张量)
(张朝阳介绍黎曼曲率张量)
由于矢量V 是任意的,因此黎曼曲率张量可以表示为克氏符沿两个方向的导数之差加上克氏符的乘积之差
![]()
黎曼曲率张量是一个四阶的张量,而能动张量是一个二阶的张量,它们之间不能直接相等。为了让这两个张量产生直接的联系,同时考虑到对称性,黎曼曲率张量可以分解成外尔张量(Weyl tensor),里奇张量(Ricci tensor)和里奇标量(Ricci scalar),其中里奇张量和里奇标量跟克氏符的关系如下
![]()
并且假设构成如下线性组合的形式
![]()
G是一个二阶对称张量,带下指标s和n的R也是一个对称张量,称之为里奇张量(Ricci tensor),最后一个标量R称之为里奇标量。
我们再回到场方程的构造问题上。能量动量张量需满足守恒的要求,即能动张量的散度为零
![]()
假设我们方程的构造也是一个线性的形式
![]()
则能动张量的守恒条件要求
![]()
用度规张量把自由指标拉到下面,可以得到
![]()
即
![]()
此时将公式(20)定义的张量G中的比例系数a除到后面的两个系数中,由此我们得到了更简洁的形式
![]()
在微分几何中存在一个关于黎曼曲率张量的恒等式,即比安基恒等式:
![]()
将上述的比安基恒等式缩并,即
![]()
可得到
![]()
再用两个指标在上的度规g作用到方程上缩并,得到
![]()
因此我们获得了系数
![]()
也计算出了场方程进一步的形式
![]()
或者写成指标全部在下方的形式
![]()
为确定待定系数c2,我们可以考虑弱场极限,此时广义相对论应回到牛顿引力,引力势能满足泊松方程
![]()
泊松方程中出现了物质的密度,而在能动量张量中,00分量代表物质的密度,这提示我们爱因斯坦场方程的00分量应该可以在弱引力下退化为牛顿引力中的泊松方程。
在弱场近似下,度规可表达为闵氏度规下的微扰
![]()
将测地线方程中加速度项的原时替换为坐标时t,并联立测地线方程
![]()
得到
![]()
其中用到了测地线的第0分量
![]()
在低速下
![]()
测地线方程进一步化简为
![]()
将度规代入克氏符中,保留一阶小量得到
![]()
我们得到加速度为
![]()
或者
![]()
此加速度与引力势的关系为
![]()
对比上面两加速度,我们得到
![]()
或
![]()
度规的微扰项的h除00分量非零外,另外的分量都为0,代入到里奇张量中得到
![]()
里奇张量的00分量和里奇标量为
![]()
将里奇张量和里奇标量代入到场方程中可直接得到
![]()
其中左边方程的最后一步用到了泊松方程。对比两边的形式可得待定系数$c_2$为
![]()
经过量纲分析
![]()
其中分母中的c平方来自于T00表示能量密度。从上式可以得到n=4,因此我们将光速c补上,得到完整的爱因斯坦场方程
![]()
史瓦西解
爱因斯坦在1915年得到了正确的场方程形式后,不期望马上得到一个非平凡的解析解,但在一年后由史瓦西(Schwarzschild)推导出了静态球对称的度规解,这让爱因斯坦十分惊讶和开心,也为后面爱因斯坦得到星光偏折、水星近日点进动和引力红移提供了基本支持。
要求解度规,可先将度规的分量形式做一个假设,进而进一步推导其形式。因考虑的时空是静态球对称的,存在沿着t方向的对称性和SO(3)对称性,所以度规的分量不会含有时间和角度,度规分量只可能是描述距离r的函数。静态时,存在沿着t方向的对称性,而且可让度规写成如下形式
![]()
这叫时轴正交坐标系(time-orthogonal coordinate system)。而球对称和静态条件可把空间部分的度规写成
![]()
因此静态球对称度规的形式可写为
![]()
而且根据上面的说法,这些度规系数只是r的函数。我们重写为更加方便的形式
![]()
满足真空爱因斯坦方程的静态球对称度规称为史瓦西真空解(Schwarzschild vacuum solution),简称史瓦西解,在物理上描述一个球对称恒星(如太阳)的外部引力场。我们将真空爱因斯坦场方程用度规缩并,得到
![]()
进而场方程变为
![]()
这被称为里奇平坦条件。由于静态球对称度规(线元)的一般形式只含两个待定一元函数 A(r) 和B(r),方程的求解变得简单:用这两个函数表出里奇张量,令其为零并对所得的关于A(r) 和B(r)的微分方程求解便可。我们首先代入度规计算克氏符
![]()
得到非零的克氏符分量
![]()
其中A’,B'表示对r求导。再把克氏符代入到黎曼曲率张量中,缩并后得到非平凡的里奇张量为
![]()
张朝阳强调,学习广义相对论应该亲自下场计算一遍上述的克氏符和里奇张量,才能找到一些学习广义相对论的感觉。由里奇平坦条件可得到如下的3 个关于待求一元函数A(r) 和B(r)的微分方程
![]()
前两个等式相减得到
![]()
即有
![]()
这个要求可将得到的最后一个微分方程化简为
![]()
其通解为
![]()
其中α为积分常数。我们得到了度规分量的表达式
![]()
重新定义坐标t,将常数C吸收进去,得到
![]()
这就是史瓦西真空解(施瓦西度规)。当r非常大的时候,史瓦西线元中的00分量可分解为平直度规和平直时空下的微扰,则此微扰必须要与前面提到的h的00分量对应起来,也就是
![]()
而点粒子的引力势能φ为
![]()
因此常数α为
![]()
由此我们得到了著名的史瓦西度规
![]()
![]() (张朝阳求解史瓦西度规)
(张朝阳求解史瓦西度规)
GPS与赤道钟走时率比较
广义相对论并非一个遥不可及的神秘理论,而是与我们的生活是息息相关的。GPS的使用就离不开广义相对论的修正,而GPS和站在地球表面的我们都在地球外面,因此只需考虑地球外部,近似视为真空球对称时空,即史瓦西度规。
我们首先考虑赤道上的观测者与太空中的观测者的走时率问题。要比较两个钟的所走过的时间就是计算世界线的线长,即原时,这个时间是在当地的观测者手握的钟表真实看到的时间,最后对表的计算时间差的时候也是计算两段世界线长度的差。在计算原时的时候,可认为是一个一个惯性观者拿着钟表跟着这一条世界线的切矢走,将他们的时间全部记录下来并累加,就得到了任意一段世界线的长度。当地球转动起来、GPS卫星绕着地球运动时,赤道上的观察者和卫星上的观察者有一个非零的相对速度,且卫星的速度比地面参考系的速度快,这会导致在地面上的观测者看到的卫星的钟所走过的时间比地面参考系的人手里握的钟所走过的时间更短,也就是说卫星上的的走时率比地面的走时率慢,这就是狭义相对论带来的时间膨胀。虽然广义相对论可以包含引力带来的时间不同和运动速度带来的时间不同,但我们仍旧区分开,让读者更加明白两种效应。我们进一步考虑广义相对论,空间的弯曲和狭义相对论的效应相反,GPS卫星的走时率会比地面参考系的走势率快。
我们主要计算引力带来的效果。考虑一个地面附近的观测者以及一个距离地面很远GPS卫星上的观测者,假设他们都是静止的,也就是只考虑r与时间t两个坐标的二维情况,可以证明两个观者处的坐标时是相同的。假设地面观者坐标r1,在t1时刻开始计时并向太空观者发送信号,太空观者坐标r2,接收到信号的时刻为t2;地面观者t1'时刻结束计时,发送信号,太空观者t2'时刻接收到信号同样结束计时,即有
![]()
做如下证明:光信号走的是类光测地线,也就是原时为零,则借助于史瓦西度规,并让光只沿着r方向运动,可得到
![]()
也就是坐标时的间隔为
![]()
由此得到要证的等式
![]()
此坐标时间并不是当地观测者手握的钟真正走的时间,而是原时τ才是。在广义相对论看起来,静止的两个观测者实际上在4维时空中做加速运动,世界线表现出一个加速度,但是我们可让无数个惯性参考系跟着这一条加速的世界线运动,使得其4维速度dx/dτ与世界线的切矢量相等。这样把这些惯性观者记录下的时间全部加起来就能计算出这条世界线的原时,也即是线长,就能得到这个加速观者所经历的时间。
![]() (张朝阳讲解坐标时和原时)
(张朝阳讲解坐标时和原时)
对于有质量粒子所走的测地线,我们仍可借助史瓦西度规,写出原时为
![]()
而静止条件要求
![]()
给出原时和坐标时的关系
![]()
在光信号传递过程中,地面参考系和GPS卫星所经历的坐标时间相同,这就给出了
![]()
其中E表示地球赤道,G表示GPS卫星。由于赤道的高度和GPS的高度不会随着原时变化而变化,此积分的结果为
![]()
我们最后计算GPS卫星和赤道处的原时差,补上光速c
![]()
代入数据
![]()
得到每天的差别为
![]()
另一方面,狭义相对论效应的贡献为
![]()
其中的相对速度为
![]()
故狭义相对论的效应为每天相差
![]()
考虑狭义相对论和广义相对论效应的总和,赤道上的观测者经历1天,GPS卫星所经历的时间比赤道上的观测者所经历的时间快
![]()
也就是说每一天的定位误差能达到
![]()
据了解,《张朝阳的物理课》于每周周五、周日中午12时在搜狐视频直播,网友可以在搜狐视频APP“关注流”中搜索“张朝阳”,观看直播及往期完整视频回放;关注“张朝阳的物理课”账号,查看课程中的“知识点”短视频;此外,还可以在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详细文章。
online betting soccerlive baccarat online casinobetting lines college football
声明:该文观点仅代表作者本人,搜狐号系信息发布平台,搜狐仅提供信息存储空间服务。
 (张朝阳讲解爱因斯坦场方程)
(张朝阳讲解爱因斯坦场方程)